A block suspended from a vertical spring is in equilibrium. Show that, the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.

A spring stores $5 \mathrm{J}$ of energy when stretched by $25 \mathrm{cm}$. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes $5$ oscillations each second, what is the mass of the block ?

A small block of mass $m$ is kept on a bigger block of mass $M$ which is attached to a vertical spring of spring constant $k$ as shown in the figure. The system oscillates vertically.

(a) Find the resultant force on the smaller block when it is displaced through a distance $x$ above its equilibrium position.

(b) Find the normal force on the smaller block at this position when is this force smallest in magnitude ?

(c) What can be the maximum amplitude with which the two blocks may oscillate together?

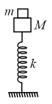
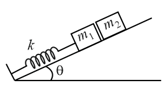
The block of mass $m_1$ shown in figure is fastened to the spring and the block of mass $m_2$ is placed against it.

(a) Find the compression of the spring in the equilibrium position.

(b) The blocks are pushed a further distance $\frac{2}{k}\left(m_1+m_2\right)g\sin \text{θ}$ against the spring and released. Find the position where the two blocks separate.

(c) What is the common speed of blocks at the time of separation?

In figure $k=100 \mathrm{N} {\mathrm{m}}^{-1}, M=1 \text{kg}$ and $F=10 \mathrm{N}$.

(a) Find the compression of the spring in the equilibrium position.

(b) A sharp blow by some external agent imparts a speed of $2 {\mathrm{ms}}^{-1}$ to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.

(c) Find the time period of the resulting simple harmonic motion.

(d) Find the amplitude.

(e) Write the potential energy of the spring when the block is at the left extreme.

(f) Write the potential energy of the spring when the block is at the right extreme.

The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy.

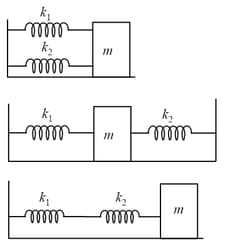
Find the time period of the oscillation of mass $m$ in $a, b, c$. The equivalent spring constant of the first pair of springs is $n\pi \sqrt{\frac{m}{k_1+k_2}}$. Find $n$.

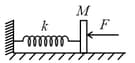
The spring is unstretched when a man starts pulling on the cord. The mass of the block is $M.$ If the man exerts a constant force $F,$ find

(a) the amplitude and the time period of the motion of the block,

(b) the energy stored in the spring when the block passes through the equilibrium position and

(c) the kinetic energy of the block at this position.