A chord of length cm is at a distance of cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of cm from the centre.

Important Questions on Circle
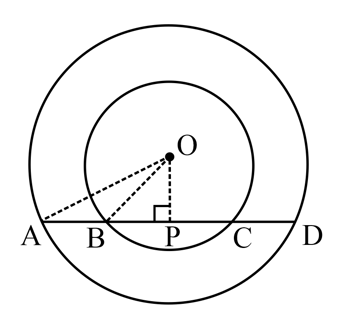
In the following figure, is a straight line. and is the centre of both circles. If ; find the length of .
In a circle of radius cm, two parallel chords of lengths are drawn. Find the distance between the chords, if both the chords are on the opposite sides of the centre.
In a circle of radius cm, two parallel chords of lengths are drawn. Find the distance between the chords, if both the chords are on the same side of the centre.
Two parallel chords are drawn in a circle of diameter cm. The length of one chord is cm and the distance between the two chords is cm; find the length of the other chord.
A chord of a circle whose centre is is bisected at by a diameter . Given cm. Calculate the length of .
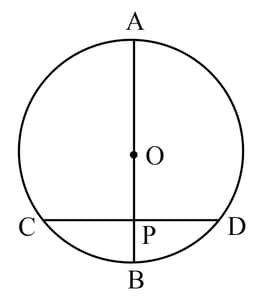
A chord of a circle whose centre is is bisected at by a diameter . Given cm. Calculate the length of .
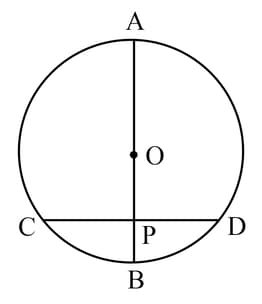
A chord of a circle whose centre is is bisected at by a diameter . Given cm. Calculate the length of .
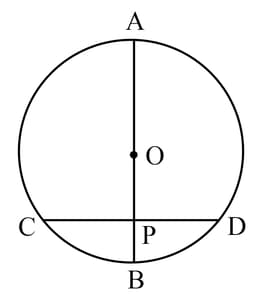
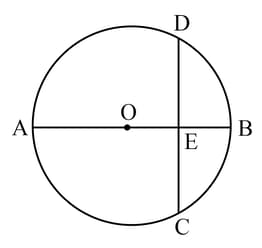
The figure, given below, shows a circle with centre in which diameter bisects the chord at point . If cm and cm, find the radius of the circle.