A circular table with the smooth horizontal surface is rotating at an angular speed $\omega$ about its axis. A groove is made on the surface along a radius, and a small particle is gently placed inside the groove at a distance $l$ from the center. Find the speed of the particle with respect to the table as its distance from the center becomes $L$.

There are two blocks of masses $m_1$ and $m_2\text{.} m_1$ is placed on $m_2$ on a table which is rotating with an angular velocity $\omega$ about the vertical axis. The coefficient of friction between the blocks is ${\mu }_1$ and between $m_2$ and table is ${\mu }_2 \left({\mu }_1<{\mu }_2\right)$. If the blocks are placed at a distance $R$ from the axis of rotation for relative sliding between the surfaces in contact, find the,

(a) frictional force at the contacting surface

(b) maximum angular speed $\mathrm{\omega }$.

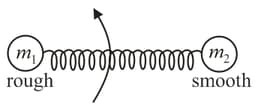
A block of mass $m_1$ connected with another block of mass $m_2$ by a light spring of natural length $l_0$ and stiffness $k$ is kept stationary on a rough horizontal surface. The coefficient of friction between $m_1$ and surface is $\mu$ and the block $m_2$ is smooth. The block $m_2$ is moved with certain speed so as to execute uniform circular motion around the block $m_1$ in horizontal plane.
Find the (a) maximum angular speed of the block $m_2$ relative to $m_1$ (b) acceleration of $m_2$ in (a).

A small block is connected to one end of two identical massless strings of length $16\frac{2}{3} \mathrm{cm}$ each with their other ends fixed to a vertical rod. If the ratio of tensions $\frac{T_1}{T_2}$ be $4:1$, then what will be the angular velocity $\omega$ of the block?

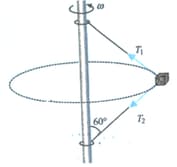
Two wires $AC$ and $BC$ are tied at $C$ of small sphere of mass $5 \mathrm{kg}$ which revolves at a constant speed $v$ in the horizontal circle of radius $1.6 \mathrm{m}$. Find the minimum value of $v$.

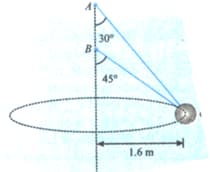
A particle of mass $m$ connected with a hanging bob of mass $M$ by an inextensible string is stationary relative to the rotating platform. The coefficient of static friction between the particle and platform is $\mu .$ Find the:
(a) maximum angular speed ${\omega }_{\max },$
(b) minimum angular speed ${\omega }_{\min }$ (for $M>\mu m$)

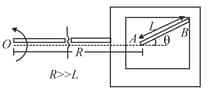
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity $\omega$ in a circular path of radius $R$. A smooth groove $AB$ of length $L(<<R)$ is made on the surface of the table. The groove makes an angle $\mathrm{\theta }$ with the radius $OA$ of the circle in which the cabin rotates. A small particle is kept at the point $A$in the groove and is released to move along $AB.$ Find the time taken by the particle to reach the point $B$.