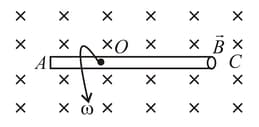
A conducting rod of length is rotated about a point in a uniform magnetic field , directed into the paper. and . Then:


Important Questions on Electromagnetic Induction
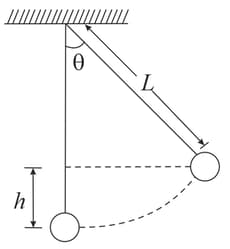
A simple pendulum with a bob of mass and conducting wire of length swings under gravity through an angle . The earth's magnetic field component in the direction perpendicular to swing is . Maximum potential difference induced across the pendulum is:
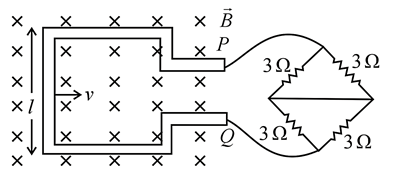
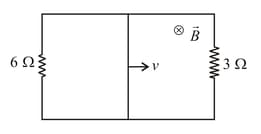
A square metallic wire loop of side and resistance of moves with a constant velocity in a magnetic field of as shown in the figure. The magnetic field is perpendicular to the plane of the loop which is connected to a network of resistances. What should be the velocity of loop so as to have a steady current of in the loop?
A conducting rod of length is moving with a uniform speed in a uniform magnetic field , directed into the paper. A capacitor of capacity is now connected to the rod, as shown in the figure. Then:
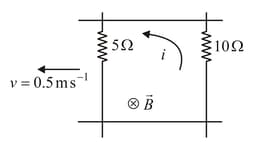
A rectangular loop, with a sliding connector of length , is situated in a uniform magnetic field , perpendicular to the plane of loop. Resistance of the connector is, Two resistances of and are connected, as shown in the figure. The external force required to keep the connector moving with a constant velocity is:
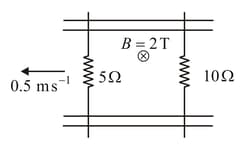
A pair of parallel conducting rails lie at right angle to a uniform magnetic field of , as shown in the figure. Two resistors of and are to slide, without friction, along the rail. The distance between the conducting rails is . Then:
The magnetic field within a cylindrical region, whose cross-section is as indicated, starts increasing at a constant rate of . The graph showing the variation of induced field with distance from the axis of cylinder is:
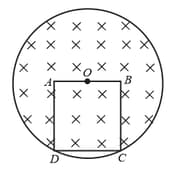
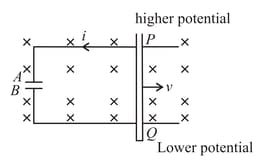
A square non-conducting loop, on a side, is placed in a magnetic field. The centre of side coincides with the centre of magnetic field. The magnetic field is increasing at the rate of . The potential difference between and is:
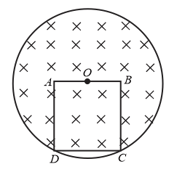
A square non-conducting loop, on a side, is placed in a magnetic field. The centre of side coincides with the centre of magnetic field. The magnetic field is increasing at the rate of . The potential difference between and is: