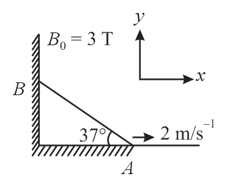
A conducting rod of length $5 \mathrm{m}$ slides in a vertical plane against two insulated perpendicular surfaces as shown. Outward uniform magnetic field $B_0=3$ Tesla exists in the region. If end $A$ of the rod is being pulled with constant speed $V_0=2 \mathrm{m} {\mathrm{s}}^{–1} \hat{i}$, then find the magnitude of induced Emf (in volt) across end $A$ and $B$ of the rod at the instant when the rod makes an angle of $\theta =37°$ with horizontal.

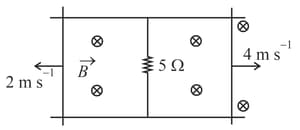
In the system shown, distance between two parallel rails are $10 \mathrm{cm}.$ Two metallic rods having resistance of $10 \mathrm{\Omega }$ and $15 \mathrm{\Omega }$ are pulled with constant speed $4 \mathrm{m} {\mathrm{s}}^{–1}$ and $2 \mathrm{m} {\mathrm{s}}^{–1}$ respectively. A uniform magnetic field of magnitude $0.01 \mathrm{T}$ is applied perpendicular to the plane of the rails. The current in the $5 \mathrm{\Omega }$ resistor is $\frac{k}{55} \mathrm{mA}.$ Value of $k$, is

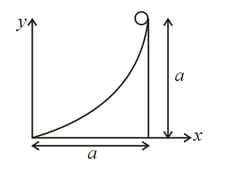
A rod of length $l$ Starts sliding down the smooth parabolic curve $y=\frac{x^2}{a}$ from $y=a$ as shown in figure. Uniform magnetic field $B_0\hat{j}$ is present in region. EMF developed across the ends of rod when it reaches the point $x=\frac{a}{\sqrt{2}}$ is $B_{0}l\sqrt{\frac{ga}{n}}.$ Value of $n$, is

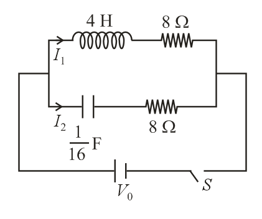
Consider the circuit shown in figure, initially capacitor is uncharged and switch is closed at $t=0.$ Value of $\frac{I_1}{I_2}$ at $t=\ln 2 \mathrm{S}$, will be

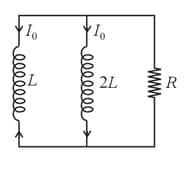
A parallel $L-R$ circuit consists of two ideal inductances $L$ and $2L$ and a resistor $R.$ At an instant the same current $I_0$ is flowing in both the inductor in the same direction. How much heat (in $\mu \mathrm{J}$) will be dissipated in resistance after a long time? $\left(L{I}_0{}^2=24 \mu \mathrm{J}\right)$

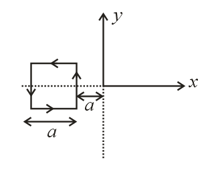
In a square loop of side length $\text{'}a\text{'},$ current $I_0$ is flowing as shown. If magnetic flux associated with region $x>0$ in $xy$ plane is $\frac{{\mu }_0{I}_{0}a}{2\pi }\ln N$, then value of $N$ is

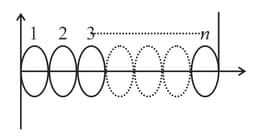
A conducting wire of length $L$ fixed at both ends is vibrating with displacement equation given by $y=2A \sin \left(kx\right) \cos \omega t.$ A constant magnetic field $B$ is present in the region as shown. If maximum value of emf induced across the wire is $\frac{4 AB\omega L}{5\pi }$, then value of $\frac{kL}{\pi }$ is

A thin superconducting ring is held above a vertical long solenoid as shown in the figure. Axis of solenoid is same as that of a ring. The cylindrically symmetric magnetic field around the ring in terms of vertical and radial component, is $B_z=B_0\left(1-\alpha z\right)$ and $B_r=B_{0}Br$ where $B_0, \alpha$ and $B$ are positive constant and $z$ and $r$ are vertical and radial components respectively. Initially plane of ring is horizontal with no current flowing through it. Mass of the ring is $m$, radius $r_0$ and self inductance $L.$ If initially, coordinates of ring are $\left(0, 0, 0\right)$ and it is released then

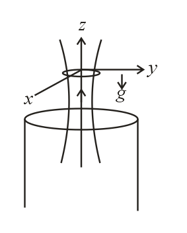
When the ring is at vertical position $z$, then current in the ring is $\frac{k{B}_0\alpha z\pi r_0^2}{L}.$ Find constant $k$ in current expression.

A thin superconducting ring is held above a vertical long solenoid as shown in the figure. Axis of solenoid is same as that of a ring. The cylindrically symmetric magnetic field around the ring in terms of vertical and radial component, is $B_z=B_0\left(1-\alpha z\right)$ and $B_r=B_{0}Br$ where $B_0, \alpha$ and $B$ are positive constant and $z$ and $r$ are vertical and radial components respectively. Initially plane of ring is horizontal with no current flowing through it. Mass of the ring is $m$, radius $r_0$ and self inductance $L.$ If initially, coordinates of ring are $\left(0, 0, 0\right)$ and it is released then

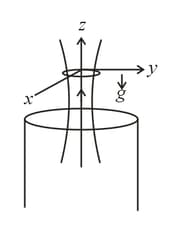
If ring is at equilibrium at vertical coordinate $z=-\frac{mgL}{2B_0^2\alpha B{\pi }^2{r}_0^N}$, then value of $N$ (Power of $r_0$) is