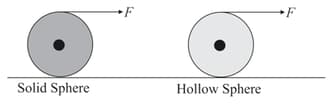
A constant horizontal force $F$ is applied on the top of a solid sphere and a hollow sphere of same mass and radius both kept on a sufficiently rough surface. Let $a_1$ and $a_2$ be their linear accelerations, then :

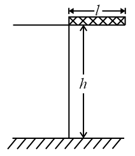
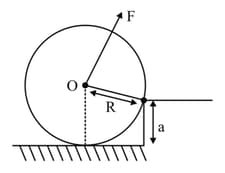
A uniform cylinder of mass $M$ and radius $R$ is to be pulled over a step of height $a\left(a<R\right)$ by applying a force $F$ at its centre $\text{'}\mathrm{O}\text{'}$ perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). The minimum value of $F$ required is:

A wheel of radius, $R$ with an axle of radius, $\frac{R}{2}$ is as shown in the figure and is free to rotate about a frictionless axis through its center and perpendicular to the page. Three forces $\left(F, F, 2 F\right)$, are exerted tangentially to the respective rims as shown in the figure.

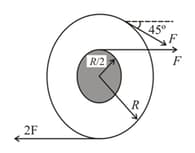
The magnitude of the net torque acting on the system is nearly, 

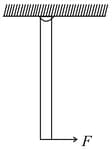
A uniform bar of mass $M$ is supported by a pivot at its top about which the bar can swing like a pendulum. If a force $F$ is applied perpendicular to the lower end of the bar as shown in figure, what is the value of $F$ in order to hold the bar in equilibrium at an angle $\left(\theta \right)$ from the vertical

A uniform rod of length $l$ and mass $m$ is free to rotate in a vertical plane about $A$. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (Moment of inertia of rod about $A$ is $\frac{m{l}^2}{3}$)

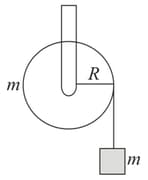
A mass $m$ is supported by a massless string wound around a uniform hollow cylinder of mass $m$ and radius $R$. If the string does not slip on the cylinder, then with what acceleration will the mass release? (Assume $g=$ acceleration due to gravity)

Consider a $20 \mathrm{kg}$ uniform circular disk of radius $0.2 \mathrm{m}$. It is pin supported at its center and is at rest initially. The disk is acted upon by a constant force $F=20 \mathrm{N}$ through a massless string wrapped around its periphery as shown in the figure.

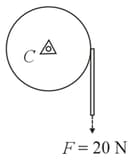
Suppose the disk makes $n$ number of revolutions to attain an angular speed of $50 \mathrm{rad} {\mathrm{s}}^{-1}$. The value of $n$, to the nearest integer, is _______ .

[Given : In one complete revolution, the disk rotates by $6.28 \mathrm{rad}$]