A container, open at top, and made of a metal sheet, is in the form of a frustum of cone of height $24 \mathrm{cm}$ with radii of its lower and upper ends as $7 \mathrm{cm}$ and $14 \mathrm{cm}$ respectively. Find the cost of milk which can completely fill the contained at the rate of rupees $25$ per $\mathrm{litre}$. Also, find the area of the metal sheet used to make the container.

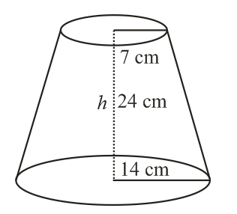
The radii of the ends of a frustum of a cone $45$cm high are $28$cm and $7$cm respectively, find the volume.

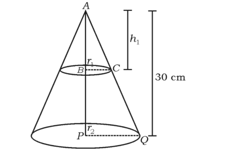
A right circular cone of height $30 \mathrm{cm}$ is cut and removed by a plane parallel to its base from the vertex. If the volume of smaller cone obtained is $\frac{1}{27}$ of the volume of the given cone. Calculate the height of the remaining part of the cone.

The radii of two circular ends of a frustum of a cone-shaped dustbin are $15 cm \& 8 cm.$ If its depth is $63 cm$ and the volume of the dustbin is $k c{m}^3$, then find the value of $k$.

The diameters of the lower and upper ends of a bucket in the form of frustum of a cone are $10 \mathrm{cm}$ and $30 \mathrm{cm}$ respectively. If its height is $24 \mathrm{cm}$, find

(i) the area of the metal sheet used to make the bucket.

(ii) Why we should avoid the bucket made by ordinary plastic? [Use $\mathrm{\pi }=3.14$]

The slant height of a frustum of a cone is $4 \mathrm{c}\mathrm{m}$ and the perimeters (circumference) of its circular ends are $18 \mathrm{c}\mathrm{m}$ and $6 \mathrm{c}\mathrm{m}$. Find the curved surface area of the frustum.

A metal cup is in the form of a frustum of a cone whose radii of bottom and top are $7 cm$ and $14 cm$ respectively, as shown in the figure. If the capacity of the cup is $2156{ \mathrm{cm}}^3$ , find the height of the cup. $\text{ (Use }\pi =\frac{22}{7}\text{ ) }$

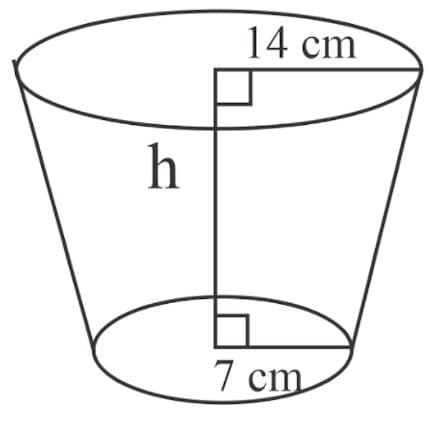
The radii of the ends of a frustum of a cone $45 \mathrm{cm}$ high are $28 \mathrm{cm}$ and $7 \mathrm{cm}$. Find its volume and the curved surface area. Take ($\mathrm{\pi }=\frac{22}{7}$)

A bucket in the form of a frustum of a cone of height $30 \mathrm{cm}$ with radii of its lower and upper ends as $10 \mathrm{cm}$ and $20 \mathrm{cm}$, respectively. Find the capacity of the bucket. Also find the cost of milk which can completely fill the bucket at the rate of $₹40$ per litre. $\left(\mathrm{Use} \mathrm{\pi }=\frac{22}{7}\right)$