A convex mirror and a concave mirror each of focal length $10 \mathrm{cm}$ are placed coaxially. They are separated by $40 \mathrm{cm}$ and their reflecting surfaces face each other. A point object is kept on the principal axis at a distance $x \mathrm{cm}$ from the concave mirror such that the final image after two reflections, first on the concave mirror, is on the object itself. Write the value of $x$ to the nearest integer.

A point object is placed on the principal axis of a concave mirror of radius of curvature $20 \mathrm{cm}$ at a distance $31 \mathrm{cm}$ from the pole of the mirror. A glass slab of thickness $3 \mathrm{cm}$ and refractive index $1.5$ is placed between object and mirror as shown in the figure.

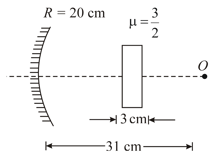
Find the distance $\left(\text{in} \mathrm{cm}\right)$ of the final image formed by the system from the mirror.

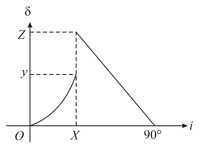
Light is incident from glass to air. The variation of the angle of deviation $\delta$ with the angle of incidence $i$ for $0<i<90°$ is shown. The refractive index of glass is $\frac{2}{\sqrt{3}}$. If the value of $\left(x+y+z\right)$ is $\frac{n\mathrm{\pi }}{6}$, then find the value of $n$.

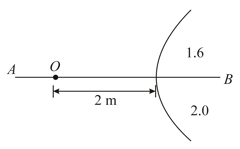
In the figure shown a point object $O$ is placed in the air. The spherical boundary of the radius of curvature $1.0 \mathrm{m}$ separates two media. $AB$ is the principal axis. The refractive index above $AB$ is $1.6$ and below $AB$ is $2.0$. Find the separation between the images $\left(\mathrm{in} \mathrm{m}\right)$ formed due to refraction at the spherical surface.

A glass hemisphere of refractive index $\frac{4}{3}$ and of the radius $4 \mathrm{cm}$ is placed on a plane mirror. A point object is placed on the axis of this sphere at a distance $d$ from $O$ as shown in the figure. If the final image is formed at infinity, then find the value of $d \mathrm{in} \mathrm{mm}$

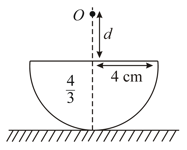
An object of height $h_0=1 \mathrm{cm}$ is moved along the principal axis of a convex lens of focal length $f=10 \mathrm{cm}$. The figure shows the variation of the magnitude of the height of the image with image distance $\left(v\right)$. Find $\left(v_2–v_1\right) \mathrm{in} \mathrm{cm}$.

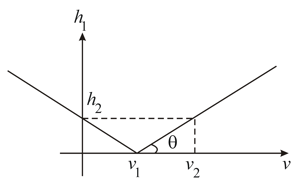
In the given figure an object $O$ is kept in the air in front of a thin plano-convex lens of the radius of curvature $10 \mathrm{cm}$. Its refractive index is $\frac{3}{2}$ and the medium towards the right of the plane surface is the water of refractive index $\frac{4}{3}$. What should be the distance $x \left(\mathrm{in} \mathrm{cm}\right)$ of the object so that the rays become parallel finally.

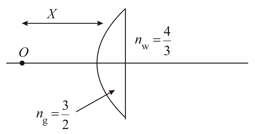
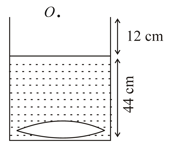
An object $O$ is kept in the air and a lens of focal length $10 \mathrm{cm} \left(\mathrm{in} \mathrm{air}\right)$ is kept at the bottom of a container which is filled up to a height $44 \mathrm{cm}$ by water. The refractive index of water is $\frac{4}{3}$ and that of glass is $\frac{3}{2}$. The bottom of the container is closed by a thin glass slab of refractive index $\frac{3}{2}$. Find the distance $\left(\mathrm{in} \mathrm{cm}\right)$ of the final image formed by the system from the bottom of the container (refer to figure shown).