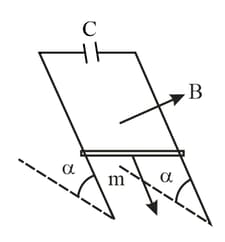
A copper connector of mass $m$ slides down two smooth copper bars, set at an angle $\alpha$ to the horizontal, due to gravity. At the top, the bars are interconnected through a capacitor, of capacitance $C$. The separation between the bars is equal to $l$. The system is located in a uniform magnetic field of induction $B$, perpendicular to the plane in which the connector slides. The resistances of the bars, the connector and the sliding contacts as well as the self-inductance of the loop, are assumed to be negligible. Find the acceleration of the connector.

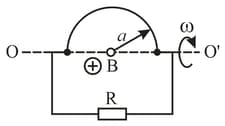
A wire shaped as a semi-circle of radius $a$, rotates about an axis $OO\text{'}$ with an angular velocity $\omega$, in a uniform magnetic field of induction $B$. The rotation axis is perpendicular to the field direction. The total resistance of the circuit is equal to $R$. Neglecting the magnetic field of the induced current, find the mean amount of thermal power being generated in the loop during a rotation period.

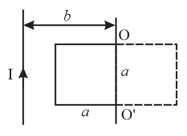
A square wire frame with side $a$ and a straight conductor carrying a constant current $I$ are located in the same plane . The inductance and the resistance of the frame are equal to $L$ and $R$ respectively. The frame was turned through $180°$ about the axis $OO\text{'}$ separated from the current-carrying conductor by a distance $b$. Find the electric charge having flown through the frame.

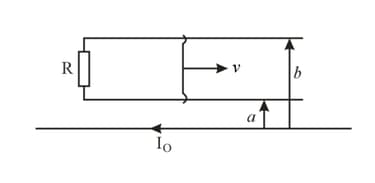
A long straight wire carries a current, $I_0$. At distances $a$ and $b$ from it there are two other wires, parallel to the former one, which are interconnected by a resistance, $R$. A connector slides without friction, along the wires, with a constant velocity, $v$. Assuming the resistances of the wires, the connector, the sliding contacts and the self-inductance of the frame to be negligible, find,
$\left(a\right)$ the magnitude and the direction of the current induced in the connector;
$\left(b\right)$ the force required to maintain the connector's velocity constant.

A conducting rod $AB$, of mass $m$, slides without friction over two long conducting rails, separated by a distance $I$ . At the left end, the rails are interconnected by a resistance $R$. The system is located in a uniform magnetic field, perpendicular to the plane of the loop. At the moment $t=0$, the rod $AB$ starts moving to the right with an initial velocity $v_0$. Neglecting the resistances of the rails and the rod $AB$, as well as the self-inductance, find,
$\left(a\right)$ the distance covered by the rod until it comes to a standstill,
$\left(b\right)$ the amount of heat generated in the resistance $R$ during this process.

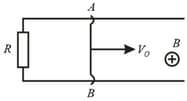
A connector $AB$ can slide, without friction, along a $\mathrm{\Pi }$-shaped conductor, located in a horizontal plane. The connector has a length $I$, mass $m$ and resistance $R$. The whole system is located in a uniform magnetic field of induction $B$, directed vertically. At the moment $t=0$, a constant horizontal force $F$ starts acting on the connector, shifting it translation-wise, to the right. Find how the velocity of the connector varies with time $t$. The inductance of the loop and the resistance of the $\mathrm{\Pi }$-shaped conductor are assumed to be negligible.

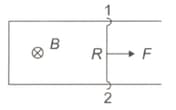
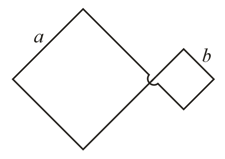
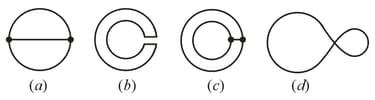
Figure illustrates plane figures made of thin conductors which are located in a uniform magnetic field, directed away from a reader, beyond the plane of the drawing. The magnetic induction starts diminishing. Find how the currents induced in these loops are directed.

A plane loop shown in the figure is shaped as two squares with sides, $a=20 \mathrm{cm}$ and $b=10 \mathrm{cm}$, and is introduced into a uniform magnetic field at right angles to the loop's plane. The magnetic induction varies with time as $B=B_0\sin \omega t$, where $B_0=10 \mathrm{mT}$ and $\omega =100 {\mathrm{s}}^{-1}$. Find the amplitude of the current induced in the loop, if its resistance per unit length is equal to $\rho =500 \mathrm{m\Omega } {\mathrm{m}}^{-1}$. The inductance of the loop is to be neglected.