A cuboidal solid gold bar of dimensions $16 \mathrm{cm}\times 11 \mathrm{cm}\times 8 \mathrm{cm}$ is melted to form a certain number of solid hemispheres of radius $2 \mathrm{cm}$ each. Find the number of such hemispheres.

The area of a trapezium is $18$ sq. cm. Its height and base are $3$ cm and $5$ cm respectively. Find the length of the side parallel to the base.

A closed wooden rectangular box made of $1$ cm thick wood has the following outer dimensions: length $22$ cm, breadth $17$ cm, and height $12$ cm. It is filled to capacity with cement. What is the volume of the cement in the box?

$\mathrm{PQRS}$ is a parallelogram and its area is $300$$\mathrm{sq}. \mathrm{cm}$. side $\mathrm{PQ}$ is extended to $X$ such that $\mathrm{PQ}=\mathrm{QX}$ .if $XS$ intersect $QR$ at $Y$, then what is the area (in $\mathrm{sq}.\mathrm{cm}$) of triangle $\mathrm{SYR}$?

$PQRS$ is a rectangle in which side of $\mathrm{PQ}$ =$24$  cm and $\mathrm{QR}$ =$16$  cm. T is a point on $RS$. What is the area (in $cm$) of the triangle $PTQ$?

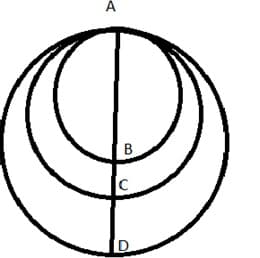
$\mathrm{ABCD}$ passes through the circle as shown in figure $\mathrm{AB}=2 \mathrm{cm}$ and $\mathrm{CD}=1 \mathrm{cm}$. If the area of the middle circle is the average of the areas of the other two circles, then what is the length (in $\mathrm{cm}$ ) of $\mathrm{BC}$?

Length and breadth of a rectangle are \(8\) \(cm\) and \(6\) \(cm\) respectively. The rectangle is cut on its four vertices such that the resulting figure is a regular octagon. What is the side (in cm) of the octagon ?

A solid hemisphere has radius $14 cm$. It is melted to form a cylinder such that the ratio of its curved surface area and total surface area is $2:3$. What is the radius of its base?

The radii of the base of a cylinder and a cone are equal and their volumes are also equal. Then the ratio of their heights is: