A current flows along a thin wire shaped as a regular polygon with sides, which can be inscribed into a circle of radius . Find the magnetic induction at the centre of the polygon. Analyze the obtained expression at .

Important Questions on ELECTRODYNAMICS
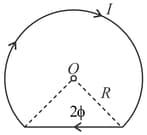
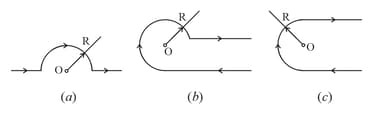
A current, flows along a thin wire shaped as shown in the figure. The radius of a curved part of the wire is equal to , the angle, . Find the magnetic induction of the field at the point (permeability of vacuum, ).
Find the magnetic induction of the field at the point of a loop, with current , whose shape is illustrated.
(a) 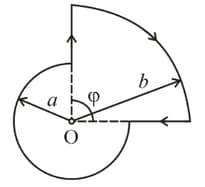
The radii and , as well as the angle are known.
(b) 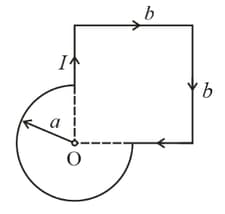
the radius and the side are known.
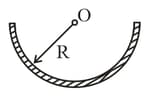
(Permeability of vacuum, )A current flows in a long straight wire with cross-section having the form of a thin half-ring of radius . Find the induction of the magnetic field at the point .
Find the magnetic induction of the field at the point if a current-carrying wire has the shape shown in figure. The radius of the curved part of the wire is , the linear parts are assumed to be very long.
Find the magnetic induction at the point , if the wire carrying a current has the shape shown in the figure.
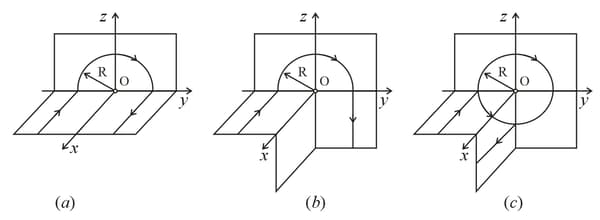
The radius of the curved part of the wire is , the linear parts of the wire are very long
(permeability of vacuum, ).