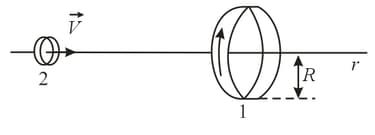
A current is flowing in a circular contour $1$ whose radius is $R$. A second contour, $2$, whose radius is much smaller than that of the first, is moving with a constant velocity, $v$ along the $r$ axis in such a manner that the planes of the contours remain parallel to each other in the course of the motion. At what distance from contour $1$ will the EMF induced in contour $2$ be maximal?

              

A certain circuit consists of a DC source with EMF $E$, an induction coil $L_1$, and a key $K_1$. No resistance is present in the circuit. Another coil, $L_2$, which is connected electrically to a resistor $R$ through a key $K_2$, is fastened to $L_1$. At some moment in time key $K_1$ is closed. After a certain time interval $K_2$ is closed. How do the current in the primary circuit (the one containing $E$), the induction emf in the secondary circuit (the one with $L_2$ and $R$), and the current in the secondary circuit vary with time?

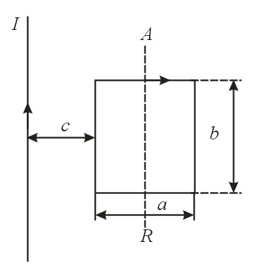
An infinitely long straight conductor and a flat rectangular contour with sides $a$ and $b$ and with $N$ turns lie in a single plane. The distance between the straight conductor and the side of the contour closest to the straight conductor is $c$. Determine the following quantities: ($1$) the mutual inductance of the conductor and the contour; ($2$) the quantity of electricity induced in the contour if the contour is rotated through $90°$ about the $AB$ axis provided that a current $I$ is flowing in the contour and the resistance of the contour is $R$ ;($3$) the work that must be done to rotate the contour through $180°$ about the $AB$ axis provided that there is current $I$ both in the long conductor and in the contour and that the sense of the current in the contour is clockwise (in the plane of the drawing).

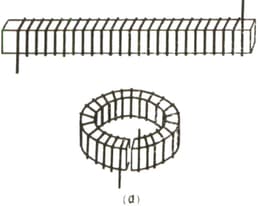
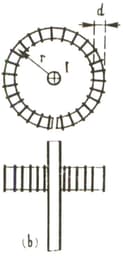
A common device used in electrical measurements is the so-called Rogowski loop. It constitutes a flexible solenoid that can be transformed into a torus if the two ends are brought together (Figure $\left(a\right)$). The leads can be connected to an $AC$ ammeter, a ballistic galvanometer*, or an oscillograph. By circling a conductor with a Rogowski loop one can measure an alternating current flowing constantly in the conductor or even isolated changes in the current, such as those that occur when the current is switched on or off or when pulses pass through the circuit. Suppose the Rogowski loop forms a toroid that encircles a conductor carrying a direct current $I$ (Figure $\left(b\right)$). The parameters of the loop are as follows: the cross-sectional area is $S$, the number of turns is $N$, the resistance of the winding is $R$, and the radius of the toroid is $r$. It is assumed that the width $d$ of the loop proper is very small compared to $r$. At a certain moment the current is switched off; the current becomes zero in a very short interval. The ballistic galvanometer in the circuit of the loop measures the quantity of electricity $Q$ that has passed through the loop (and the galvanometer). How can one find the current $I$ that was flowing in the conductor prior to switch-off knowing the values of the above-mentioned parameters?

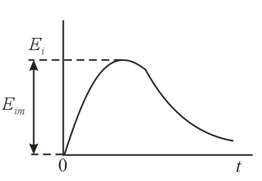
A flat coil with a cross-sectional area $S$ and with $N$ turns is placed in a magnetic field. The leads of the coil are connected to an oscillograph. When the coil is moved out of the field, an induction emf is generated in it, and the oscillograph of this emf is shown in the figure. How do the maximal value of the emf, $E_{1\mathrm{m}}$, and the area under the curve depending on the rate with which the coil is moved out of the field?

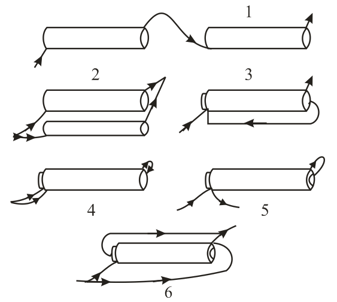
Suppose that we have two solenoids of the same length. Their diameters differ only to the extent to which one can be fitted onto the other. The inductances of the two solenoids can be considered the same and equal to $L$. Here are the ways in which the solenoids can be connected:

($1$) the solenoids are connected in series and are separated by a large distance;

($2$) the solenoids are connected in parallel and are separated by a large distance;

($3$) the solenoids are connected in series, one is fitted onto the other, and the senses of the turns coincide;

($4$) the solenoids are connected in parallel, one is fitted onto the other, and the senses of the turns coincide;

($5$) the solenoids are connected in series, one is fitted onto the other, and the senses of the turns are opposite;

($6$) the solenoids are connected in parallel, one is fitted onto the other, and the senses of the turns are opposite.

Determine the total inductance for each of the above cases.

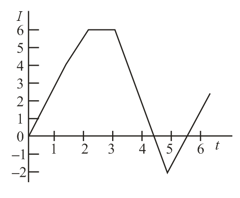
The current flowing in a certain inductance coil varies in time according to the curve shown schematically in the figure. Draw the curve representing the induced emf as a function of time (also schematically).

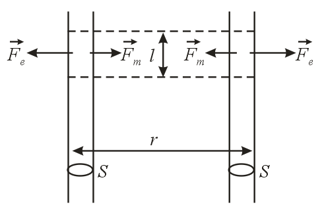
Two similar parallel electron beams point in the same direction. The linear dimensions of the cross section of each beam are small compared to the distance between the beams. Suppose that $v$ is the electron velocity and $n$ is the electron concentration in either beam. In a coordinate system with respect to which the electrons are in motion there are two types of interactions, the electrostatic and the magnetic. Which of the two is greater in magnitude?