A curve has equation; $y=27x-\frac{4}{(x+2{)}^2}$. Show that the curve has a stationary point at $x=-\frac{8}{3}$ and determine its nature.

A watermelon is assumed to be spherical in shape while it is growing. Its mass, $M$ kg, and radius, $r$ cm, are related by the formula $M=k{r}^3$, where $k$ is a constant. It is also assumed that the radius is increasing at a constant rate of $0.1$ centimetres per day. On a particular day the radius is $10$ cm and the mass is $3.2$ kg. Find the value of $k$ and the rate at which the mass is increasing on this day.

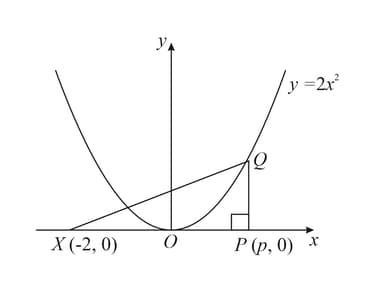
The diagram shows the curve $y=2x^2$ and the points $X(-2,0)\text{ and }P(p,0)$. The point $Q$ lies on the curve and $PQ$ is parallel to the $y-$axis. Express area $A$ of triangle $XPQ$ in terms of $p$.

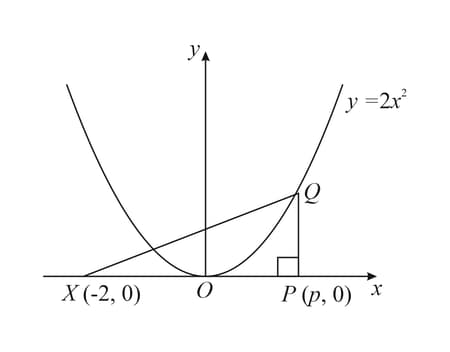
The diagram shows the curve $y=2x^2$ and the points $X(-2,0)\text{ and }P(p,0)$. The point $Q$ lies on the curve and $PQ$ is parallel to the $y-$axis.

The point $P$ moves along the $x-$axis at a constant rate of $0.02$ units per second and $Q$ moves along the curve so that $PQ$ remains parallel to the $y-$axis. Find the rate at which area $A$ increasing when $p=2$.[Write your answer excluding units]

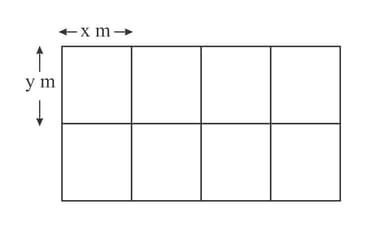
A farmer divides a rectangular piece of land into 8 equal-sized rectangular sheep pens as shown in the diagram. Each sheep pen measures $x$ m by $y$ m and is fully enclosed by metal fencing. The farmer uses $480$ m of fencing. Show that the total area of land used for the sheep pens $A {\mathrm{m}}^2$, is given by $A=384x-9.6x^2$.

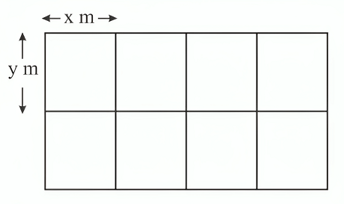
A farmer divides a rectangular piece of land into 8 equal-sized rectangular sheep pens as shown in the diagram. Each sheep pen measures $x$ m by $y$ m and is fully enclosed by metal fencing. The farmer uses $480$ m of fencing. Given that $x$ and $y$ can vary, find the dimensions of each sheep pen for which the value of $A$ is a maximum. (There is no need to verify that the value of $A$ is a maximum.).

The variables $x,y\text{ and }z$ can take only positive values and are such that $z=3x+2y\text{ and }xy=600$. Show that $z=3x+\frac{1200}{x}$. Find the stationary value of $z$ and determine its nature.

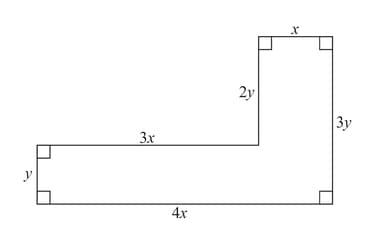
The diagram shows the dimensions in metres of an $L-$shaped garden. The perimeter of the garden is $48$ m. Find an expression for $y$ in terms of $x$.

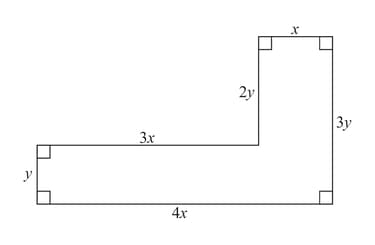
The diagram shows the dimensions in metres of an $L-$shaped garden. The perimeter of the garden is $48$ m. Given that the area of the garden is $A {\mathrm{m}}^2$, show that, $A=48x-8x^2$.