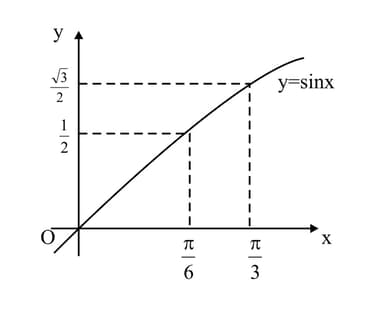
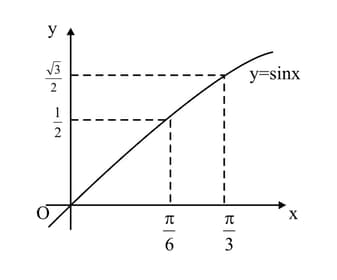
A curve is such that d y d x = 1 - 3 sin 2 x . Given that the curve passes through the point π 4 , 0 find the equation of the curve.

Given that, we have: d y d x = 1 - 3 sin 2 x Apply integration on both sides, then we get: y = x + 3 2 cos 2 x + c [Since, integration is inverse process of differentiation and ∫ sin ( a x ) d x = - 1 a cos ( a x ) + c ] And also, given that, the above curve is passing through the point π 4 , 0 , then 0 = π 4 + 3 2 cos 2 π 4 + c ⇒ 0 = π 4 + 3 2 cos π 2 + c ⇒ c = - π 4 Hence, the required equation of the curve is y = x + 3 2 cos 2 x - π 4 .

A curve is such that d y d x = 1 - 3 sin 2 x . Given that the curve passes through the point π 4 , 0 find the equation of the curve.

Given that, we have: d y d x = 1 - 3 sin 2 x Apply integration on both sides, then we get: y = x + 3 2 cos 2 x + c [Since, integration is inverse process of differentiation and ∫ sin ( a x ) d x = - 1 a cos ( a x ) + c ] And also, given that, the above curve is passing through the point π 4 , 0 , then 0 = π 4 + 3 2 cos 2 π 4 + c ⇒ 0 = π 4 + 3 2 cos π 2 + c ⇒ c = - π 4 Hence, the required equation of the curve is y = x + 3 2 cos 2 x - π 4 .

A curve is such that d 2 y d x 2 = - 12 sin 2 x - 2 cos x . Given that d y d x = 4 when x = 0 and that the curve passes through the point π 2 , - 3 , find the equation of the curve.

Given that, we have: d 2 y d x 2 = - 12 sin 2 x - 2 cos x Apply integration on both sides, then we get: d y d x = 12 2 cos 2 x - 2 sin x + c , where c = constant of integration [Since, integration is inverse process of differentiation] ⇒ d y d x = 6 cos 2 x - 2 sin x + c Given that, d y d x = 4 , when x = 0 , then 4 = 6 cos 0 - 2 sin 0 + c ⇒ 4 = 6 + c ⇒ c = - 2 Thus, d y d x = 6 cos 2 x - 2 sin x - 2 Again apply integration on both sides, then we get: y = 6 2 sin 2 x + 2 cos x - 2 x + c 1 ⇒ y = 3 sin 2 x + 2 cos x - 2 x + c 1 , where c 1 = constant of integration And also, given that, the above curve is passing through the point π 2 , - 3 , then - 3 = 3 sin 2 π 2 + 2 cos π 2 - 2 π 2 + c 1 ⇒ - 3 = - π + c 1 ⇒ - 3 + π = c 1 Hence, the required equation of the curve is y = 3 sin 2 x + 2 cos x - 2 x + π - 3 .

The point π 2 , 5 lies on the curve for which d y d x = 4 sin 2 x - π 2 . Find the equation of the normal to the curve at the point where x = π 3 .

Given that, we have: d y d x = 4 sin 2 x - π 2 Apply integration on both sides, then we get: y = - 4 2 cos 2 x - π 2 + c , where c = constant of integration [Since, integration is inverse process of differentiation] ⇒ y = - 2 cos 2 x - π 2 + c And also, given that, the above curve is passing through the point π 2 , 5 , then 5 = - 2 cos 2 × π 2 - π 2 + c ⇒ 5 = - 2 cos π - π 2 + c ⇒ 5 = - 2 cos π 2 + c ⇒ 5 = c Hence, the required equation of the curve is y = 5 - 2 cos 2 x - π 2 . Now, at x = π 3 , then the slope of the tangent is d y d x x = π 3 = 4 sin 2 π 3 - π 2 = 4 sin π 6 = 4 × 1 2 = 2 Therefore, the slope of the normal will be - 1 2 [If slope of the tangent is m , then the slope of the normal will be - 1 m ] Now, at x = π 3 , then y = 5 - 2 cos 2 × π 3 - π 2 ⇒ y = 5 - 2 cos π 6 ⇒ y = 5 - 2 × 3 2 ⇒ y = 5 - 3 Now, the equation of the normal at π 3 , 5 - 3 is y - 5 - 3 = - 1 2 x - π 3 ⇒ 2 y - 10 - 2 3 = - x + π 3 ⇒ x + 2 y = 10 - 2 3 + π 3 Hence, the required equation of the normal is x + 2 y = 10 - 2 3 + π 3 .

The diagram shows the curve y = sin x . The points π 6 , 1 2 and π 3 , 3 2 lie on the curve. Find the exact value of ∫ π 6 π 3 sin x d x .

Given that, we have, Now, we are also, given that, ∫ π 6 π 3 sin x d x = - cos x π 6 π 3 = - cos π 3 - - cos π 6 = - 1 2 + 3 2 = 1 2 ( 3 - 1 ) Hence, the exact value of ∫ π 6 π 3 sin x d x = 1 2 ( 3 - 1 ) .

The diagram shows the curve y = sin x . The points π 6 , 1 2 and π 3 , 3 2 lie on the curve. Show that ∫ 1 2 3 2 sin - 1 y d y = π 12 ( 2 3 - 1 ) - 3 - 1 2 .

Given that, we have, We need to show that, ∫ 1 2 3 2 sin - 1 y d y = π 12 ( 2 3 - 1 ) - 3 - 1 2 Consider LHS, I = ∫ 1 2 3 2 sin - 1 y d y ⇒ I = sin - 1 y ∫ 1 2 3 2 1 d y - ∫ 1 2 3 2 d d y sin - 1 y ∫ 1 2 3 2 1 d y d y [Using Integration By Parts] ⇒ I = y sin - 1 y 1 2 3 2 - ∫ 1 2 3 2 1 1 - y 2 y d y ⇒ I = y sin - 1 y 1 2 3 2 - ∫ 1 2 3 2 - 1 2 - 2 y 1 - y 2 d y ⇒ I = y sin - 1 y 1 2 3 2 + 1 2 ∫ 1 2 3 2 - 2 y 1 - y 2 d y ⇒ I = y sin - 1 y 1 2 3 2 + 1 2 × 2 1 - y 2 1 2 3 2 ⇒ I = y sin - 1 y 1 2 3 2 + 1 - y 2 1 2 3 2 ⇒ I = 3 2 sin - 1 3 2 - 1 2 sin - 1 1 2 + 1 - 3 2 2 - 1 - 1 2 2 ⇒ I = 3 2 × π 3 - 1 2 × π 6 + 1 - 3 4 - 1 - 1 4 ⇒ I = π 3 6 - π 12 + 1 2 - 3 2 ⇒ I = π 12 ( 2 3 - 1 ) - 3 - 1 2 = RHS Hence, proved.

The diagram shows the curve y = cos x . The points π 4 , 2 2 and π 3 , 1 2 lie on the curve. Find the exact value of ∫ π 4 π 3 cos x d x .

Given that, we have, Now, we are also, given that, ∫ π 4 π 3 cos x d x = sin x π 4 π 3 = sin π 3 - sin π 4 = 3 2 - 1 2 = 1 2 ( 3 - 2 ) Hence, the exact value of ∫ π 4 π 3 cos x d x = 1 2 ( 3 - 2 ) .

E M B I B E

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 5 - Integration>EXERCISE 5C>Q 4

MEDIUM

AS and A Level

IMPORTANT

Earn 100

A curve is such that $\frac{d y}{d x} = 1 - 3 \sin 2 x$ . Given that the curve passes through the point $(\frac{π}{4}, 0)$ find the equation of the curve.

Important Questions on Integration

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 5 - Integration>EXERCISE 5C>Q 5

A curve is such that $\frac{d^{2} y}{d x^{2}} = - 12 \sin 2 x - 2 \cos x$ . Given that $\frac{d y}{d x} = 4 when x = 0$ and that the curve passes through the point $(\frac{π}{2}, - 3)$ , find the equation of the curve.

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 5 - Integration>EXERCISE 5C>Q 6

The point $(\frac{π}{2}, 5)$ lies on the curve for which $\frac{d y}{d x} = 4 \sin (2 x - \frac{π}{2})$ . If the equation of the curve is $y = k - 2 \cos (2 x - \frac{π}{2})$ , then find the value of $k$ .

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 5 - Integration>EXERCISE 5C>Q 6

The point $(\frac{π}{2}, 5)$ lies on the curve for which $\frac{d y}{d x} = 4 \sin (2 x - \frac{π}{2})$ . Find the equation of the normal to the curve at the point where $x = \frac{π}{3}$ .

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 5 - Integration>EXERCISE 5C>Q 7

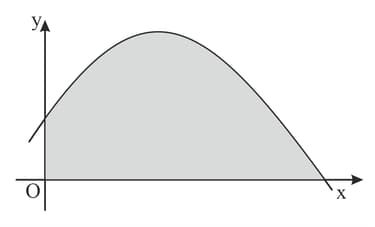
Question Image

The diagram shows part of the curve $y = 1 + \sqrt{3} \sin 2 x + \cos 2 x$ . If the exact value of the area of the shaded region is $\frac{π}{2} + \sqrt{p}$ , then find the value of $p$ .

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 5 - Integration>EXERCISE 5C>Q 8

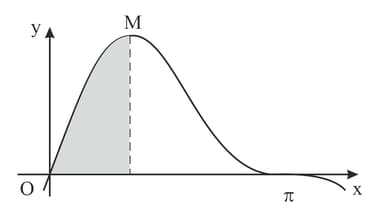
Question Image

The diagram shows the curve $y = 3 \sin 2 x + 6 \sin x$ and its maximum point $M$ . Find the exact area of the shaded region.

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 5 - Integration>EXERCISE 5C>Q 9

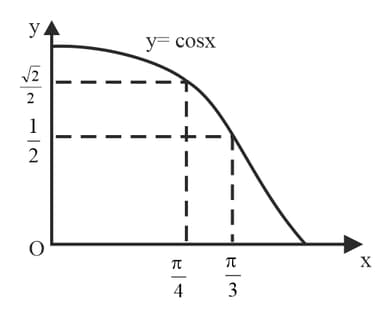
Question Image

The diagram shows the curve $y = \sin x$ . The points $(\frac{π}{6}, \frac{1}{2}) and (\frac{π}{3}, \frac{\sqrt{3}}{2})$ lie on the curve. Find the exact value of $\int_{\frac{π}{6}}^{\frac{π}{3}} \sin x d x$ .

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 5 - Integration>EXERCISE 5C>Q 9

Question Image

The diagram shows the curve $y = \sin x$ . The points $(\frac{π}{6}, \frac{1}{2}) and (\frac{π}{3}, \frac{\sqrt{3}}{2})$ lie on the curve. Show that $\int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}} (\sin^{- 1} y) d y = \frac{π}{12} (2 \sqrt{3} - 1) - \frac{\sqrt{3} - 1}{2}$ .

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 5 - Integration>EXERCISE 5C>Q 10

Question Image

The diagram shows the curve $y = \cos x$ . The points $(\frac{π}{4}, \frac{\sqrt{2}}{2}) and (\frac{π}{3}, \frac{1}{2})$ lie on the curve. Find the exact value of $\int_{\frac{π}{4}}^{\frac{π}{3}} \cos x d x$ .