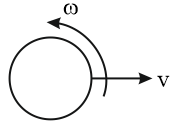
A cylinder moves with linear velocity $v$ to the right and angular velocity ω in the anticlockwise direction. The cylinder was initially at rest. The cylinder does not perform pure rolling and stops after some time. What will be the radius of the cylinder?

 

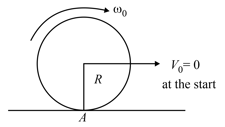
A solid sphere is set into rotation at an angular velocity ${\text{ω}}_0$ and it is then, placed on a rough horizontal surface. The ratio of distances covered by rotational and translational motions up to the start of the pure rolling is (assume uniformly accelerated motion up to start of pure rolling):

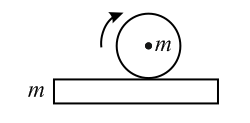
A sphere of mass $m$ is given some angular velocity about a horizontal axis through its center and gently placed on a plank of mass $m.$ The coefficient of friction between the two is $\mu$. The plank rests on a smooth horizontal surface. The initial acceleration of the center of sphere relative to the plank will be:

A cylinder $A$ rolls without slipping on a plank $B$. The velocities of center of the cylinder and that of the plank are $4 \mathrm{m} {\mathrm{s}}^{-1}$ and $2 \mathrm{m} {\mathrm{s}}^{-1}$ respectively in the same direction with respect to the ground. The angular velocity of the cylinder, if its radius is$1 \mathrm{m}$ is

A rigid body undergoing uniform pure rolling encounters horizontal tracks $AB$ and $BC$ as shown $AB$ is a smooth layer of ice and $BC$ is a rough surface with $\mu =1.$ Both $AB$ and $BC$ are rigid tracks. Which of the following statements are correct?

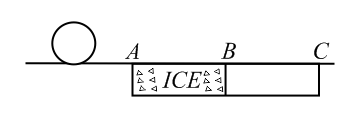
$\left(1\right)$ The body will slow down over $BC$.

$\left(2\right)$ The body will start slipping on $AB$.

$\left(3\right)$ The body remains in pure rolling over the whole stretch $AC$.

$\left(4\right)$ The angular velocity of the body remains constant over the whole stretch $AC$.

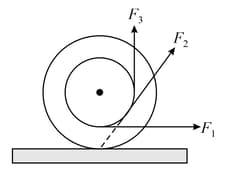
A spool is resting on a horizontal rough table. Forces $F_1, F_2$ and $F_3$ are applied separately as shown. $F_1, F_2, F_3$ all are applied tangentially to the inner circle. $F_1$ is horizontal, $F_3$ is vertical and $F_2$ is passing through the point of contact of spool and table. The correct statement is (assuming that there is no sliding)?

A cylinder of mass $m$ is placed on the edge of a plank of the same mass and length $4\mu g^2$ placed on the smooth horizontal surface, where $\mu$is the coefficient of friction between cylinder and plank and $t$ is the time at which pure rolling starts. The cylinder is given an impulse at, $t=0$ which imparts it a velocity $V_0(\mathrm{m} {\mathrm{s}}^{-1})$. The time in which pure rolling starts will be

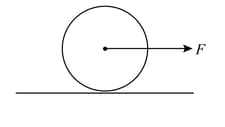
A uniform disc of radius $R$ is resting on a table on its rim. The coefficient of friction between disc and table is $\mu$ (see figure). Now, the disc is pulled with a force $F$ as shown in the figure. What is the maximum value of $F$ for which the disc rolls without slipping?

A $2\mathrm{ }\mathrm{kg}$ uniform cylinder is placed on a plank of mass $4\mathrm{ }\mathrm{kg}$ which in turn rests on a smooth horizontal plane. A constant horizontal force of $20\mathrm{ }\mathrm{N}$ is applied on the plank. If no slipping occurs between cylinder and plank obtain the acceleration of the cylinder and the plank.