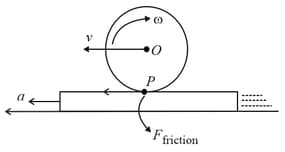
A disc of mass $M$ and radius $R$ rolls without slipping on a horizontal surface (see figure).

If the speed of its centre is $v_0$, then the magnitude of the angular momentum of the disc about a fixed point $P$ at a height $5\mathrm{R}/2$ above the horizontal surface

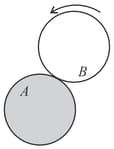
A flat surface of a thin uniform disk $A$ of radius $R$ is glued to a horizontal table. Another thin uniform disk $B$ of mass $M$ and with the same radius $R$ rolls without slipping on the circumference of $A$, as shown in the figure. A flat surface of $B$ also lies on the plane of the table. The center of mass of $B$ has fixed angular speed $\omega$ about the vertical axis passing through the center of $A$. The angular momentum of $B$ is $nM\omega R^2$ with respect to the center of $A$. Which of the following is the value of $n$?

​​​​​​​

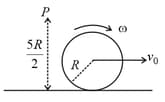
A small roller of diameter $20 \mathrm{cm}$ has an axle of diameter $10 \mathrm{cm}$ (see figure below on the left). It is on a horizontal floor and a meter scale is positioned horizontally on its axle with one edge of the scale on top of the axle (see figure on the right). The scale is now pushed slowly on the axle so that it moves without slipping on the axle, and the roller starts rolling without slipping. After the roller has moved $50 \mathrm{cm},$ the position of the scale will look like (figures are schematic and not drawn to scale)

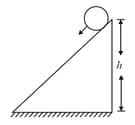
A solid cylinder of mass $m$ and radius $R$ rolls down inclined plane without slipping. The speed of its $C.M.$ when it reaches the bottom is___

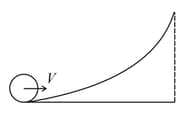
A small object of uniform density rolls up a curved surface with an initial velocity $v$. It reaches up to a maximum height of $\frac{3v^2}{4g}$ with respect to the initial position. The object is 

A solid sphere and solid cylinder of identical radii approach an incline with the same linear velocity (see figure). Both roll without slipping all throughout. The two climb maximum heights $h_{sph}$ and $h_{cyl}$ on the incline. The ratio $\frac{h_{sph}}{h_{cyl}}$ is given by:

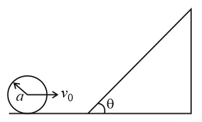
A sphere of radius $a$ and mass $m$ rolls along a horizontal plane with constant speed $v_0$. It encounters an inclined plane at angle $\theta$ and climbs upward. Assuming that it rolls without slipping, how far up the sphere will travel?