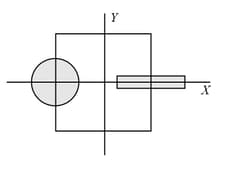
A disk of radius $\frac{a}{4}$ having a uniformly distributed charge $6 \mathrm{C}$ is placed in the $x-y$ plane with its centre at $\left(-\frac{a}{2}, 0, 0\right)$. A rod of length $a$ carrying a uniformly distributed charge $8 \mathrm{C}$ is placed on the $x$-axis from $x=\frac{a}{4}$ to $x=\frac{5a}{4}$. Two point charges $-7 \mathrm{C}$ and $3 \mathrm{C}$ are placed at $\left(\frac{a}{4},-\frac{a}{4}, 0\right)$ and $\left(-\frac{3a}{4},\frac{3a}{4}, 0\right)$, respectively. Consider a cubical surface formed by six surfaces, $x=\pm \frac{a}{2}, y=\pm \frac{a}{2}, z=\pm \frac{a}{2}$. The electric flux through this cubical surface is,

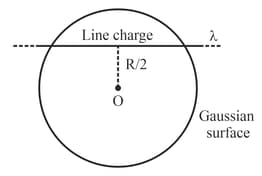
Find the flux through the Gaussian surface, given that the radius of the circle is $R$.

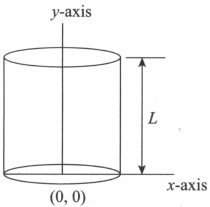
A long charged wire is kept on $y$-axis, one end at origin. Its linear charge density varies as, $\lambda ={\lambda }_{0}y.$ Calculate the electric flux passing through the cylinder.

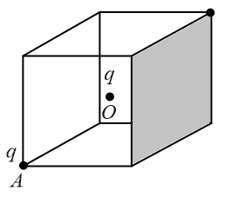
Two-point charges, each of magnitude $q$, are kept at the centre of the cube $O$ and vertex $A$. Find the flux through the shaded face.

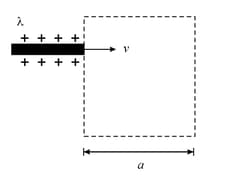
The figure below shows an imaginary cube of side $a.$ A uniformly charged rod of length $\frac{a}{2}$ moves towards the right at a constant speed $v.$ At $t=0,$ the right end of the rod just touches the left face of the cube. Plot a graph between electric flux $\left({\varphi }_{\mathrm{E}}\right)$ passing through the cube versus time $\left(t\right)$.

The figure shows a cube of side $l$ with edges parallel to the axes. The electric field is in positive $y$ direction but its magnitude changes such that it is $\frac{15}{{\epsilon }_0{l}^2}$ at the bottom face and $\frac{5}{{\epsilon }_0{l}^2}$ at the top face in SI units. Find the charge enclosed by the cube.

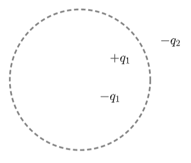
Consider the charge configuration and spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field is due to