A disk with a rotational inertia of $7.00 \mathrm{kg} {\mathrm{m}}^2$ rotates like a merry-go-round while undergoing a variable torque given by $\tau =(5.00+2.00t) \mathrm{N} \mathrm{m}$. At time $t=1.00 \mathrm{s}$ its angular momentum $5.00 \mathrm{kg} {\mathrm{m}}^2 {\mathrm{s}}^{-1}$. What is its angular momentum at $t=5.00 \mathrm{s}$?

Figure shows a rigid structure consisting of a circular hoop of radius $R$ and mass $m$ and a square made of four thin bars, each of length $R$ and mass $m$. The rigid structure rotates at a constant speed about a vertical axis, with a period of rotation of $2.5 \mathrm{s}$. Assuming $R=0.50 \mathrm{m}$ and $m=2.0 \mathrm{kg}$, calculate (a) the structure's rotational inertia about the axis of rotation and (b) its angular momentum about that axis.

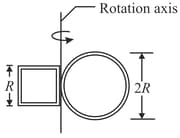
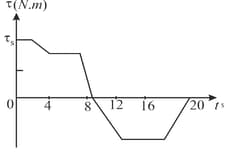
Figure gives the torque $\tau$ that acts on an initially stationary disk that can rotate about its centre like a merry-go-round. The scale on the $\tau$ axis is set by ${\tau }_{\mathrm{s}}=4.0 \mathrm{N}-\mathrm{m}$. What is the angular momentum of the disk about the rotation axis at times (a) $t=7.0 \mathrm{s}$ and (b) $t=20 \mathrm{s}$?

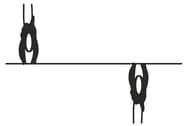
In the figure shown below, two skaters, each of mass $50 \mathrm{kg}$ approach each other along parallel paths separated by $3.0 \mathrm{m}$. They have opposite velocities of $1.4 \mathrm{m} {\mathrm{s}}^{-1}$ each. One skater carries one end of a long pole of negligible mass and the other skater grabs the other end as she passes. The skaters then rotate around the center of the pole. Assume that the friction between the skates and the ice is negligible. What are (a) the radius of the circle, (b) the angular speed of the skaters and (c) the kinetic energy of the two-skater system? Next, the skaters pull along the pole until they are separated by $1.0 \mathrm{m}$. What then are (d) their angular speed and (e) the kinetic energy of the system? (f) What provided the energy for the increased kinetic energy?

A track is mounted on a large wheel that is free to turn, with negligible friction, about a vertical axis (figure below). A toy train of mass $m$ is placed on the track and, with the system initially at rest, the train's electrical power is turned on. The train reaches speed $0.15 \mathrm{m} {\mathrm{s}}^{-1}$ with respect to the track. What is the wheel's angular speed if its mass is $1.1 \mathrm{m}$ and its radius is $0.43 \mathrm{m}$? (Treat it as a hoop and neglect the mass of the spokes and hub)

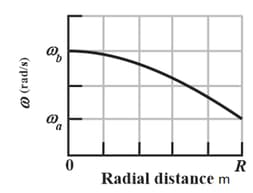
A Texas cockroach walks from the center of a circular disk (that rotates like a merry-go-round without external torques) out to the edge at radius, $R$. The angular speed of the cockroach-disk system for the walk is given in the figure ${\omega }_a=5.0 \mathrm{rad} {\mathrm{s}}^{-1}$and${\omega }_{\mathrm{b}}=6.0 \mathrm{rad} {\mathrm{s}}^{-1}$. After reaching $R$, what fraction of the rotational inertia of the disk does the cockroach have?