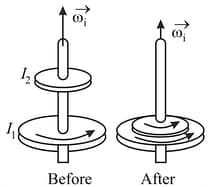
A disk with moment of inertia $I_1$ rotates about a frictionless, vertical axle with angular speed ${\omega }_i$. A second disk, this one having moment of inertia $I_2$ and initially not rotating, drops onto the first disk (figure). Because of friction between the surfaces, the two eventually reach the same angular speed ${\omega }_f$ , calculate ${\omega }_f$.

A man of mass $100\mathrm{}\mathrm{k}\mathrm{g}$ stands at the rim of a turntable of radius $2\mathrm{}\mathrm{m}$ and moment of inertia $4000 \mathrm{k}\mathrm{g} {\mathrm{m}}^2$ mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of $1\mathrm{m} {\mathrm{s}}^{-1}$ relative to the earth.
(a) With what angular velocity and in what direction does the turntable rotate?
(b) Through what angle will table have rotated when the man reaches his initial position on the turntable?
(c) Through what angle will table have rotated when the man reaches his initial position relative to the earth?

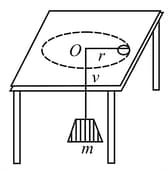
A thread is passing through a hole at the centre of a frictionless table. At the upper end a block of mass $0.5\mathrm{}\mathrm{k}\mathrm{g}$ is tied and a block of mass $8.0\mathrm{}\mathrm{k}\mathrm{g}$ is tied at the lower end which is freely hanging. The smaller mass is rotated on the table with a constant angular velocity about the axis passing through the hole so as to balance the heavier mass. If the mass of the hanging block is changed from $8.0\mathrm{}\mathrm{k}\mathrm{g}$ to $1.0\mathrm{}\mathrm{k}\mathrm{g}$ , what is the fractional change in the radius and the angular velocity of the smaller mass so that it balances the hanging mass again?

A uniform rod of mass $m$ and length $l$ is acted upon by the forces $F_1$ and $F_2.$ Find that:

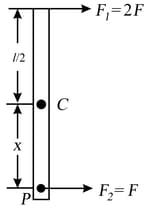
(a) linear and angular acceleration of the rod.

(b) value of $x$ for which the point $P$ does not accelerate.

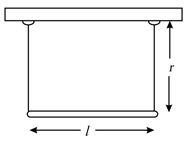
A uniform rod of mass $M$ and length $l$ is suspended by two vertical inextensible strings as shown in figure. Calculate tension in left string at the instant, when right string snaps.

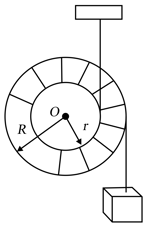
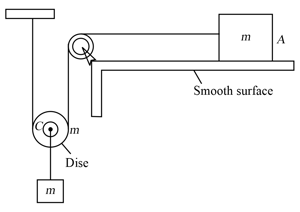
In the figure $A$ and $B$ are identical blocks, each of mass $m$ and $C$ is a circular disc of equal mass $m$. Pulley is massless and ffictionless and thread is inextensible. Neglecting friction, find the acceleration of block $A$ and $B$.

A light thread has been tightly wrapped around a disc of mass $M$ and radius $R$. The disc has been placed on a smooth table, lying flat as shown. The other end of the string has been attached to a mass $m$ as shown. The system is released from rest. Find the acceleration of the disc and block.

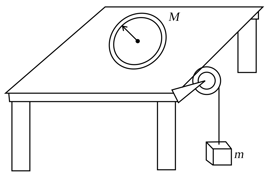
In the arrangement shown, the double pulley has a mass $M$ and the two massless threads have been tightly wound on the inner (radius $=r$) and outer circumference (radius $R=2r$). The block shown has a mass $4M$ . The moment of inertia of the double pulley system about a horizontal axis passing through its centre and perpendicular to the plane of the figure is $I=\frac{M{r}^2}{2}$ . Find acceleration of the center of the pulley after the system is released.
​​​​​​​