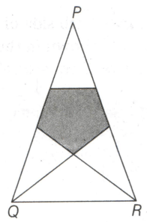
A few of the sides of a regular pentagon are extended in such a way that it forms an isosceles triangle as shown in the given diagram. If the perimeter of the pentagon is $10 \mathrm{cm},$ what is the perimeter of the isosceles triangle $\mathrm{PQR} ?$

In the following figure, if the area of the shaded region (the smaller pentagon) is $\left(\frac{7-3\sqrt{5}}{2}\right) \mathrm{sq}. \mathrm{cm},$ find the area of the larger regular pentagon.

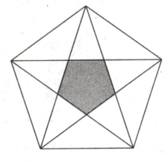
In the following figure when all the five diagonals of a regular pentagon are drawn they form another small pentagon at the centre which is shown as a shaded region. If each side of the larger (original) pentagon measures $1$ inch, and $\phi =\frac{\sqrt{5}+1}{2},$ find the ratio of the area of larger pentagon to the area of smaller pentagram in terms of $\phi .$

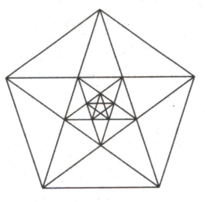
In the given figure the diagonals of a pentagon form another pentagon, and the diagonals of this pentagon form another pentagon, and then once again the diagonals of this pentagon form another pentagon at the centre. If the each side of the smallest pentagon is $1$ unit and $\phi =\frac{1+\sqrt{5}}{2},$ find each side of the largest (original) pentagon in terms of $\phi .$

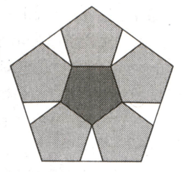
A larger regular pentagon contains $6$ smaller pentagons of the same size, as shown in the following diagram. If each side of each of the congruent pentagons is $1 \mathrm{cm},$ find the total area $\mathrm{A}$ (in $\mathrm{sq}. \mathrm{cm}$ ) covered by the larger pentagon.

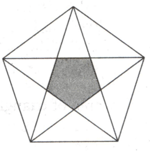
In the following figure a regular pentagon inscribes a regular pentagram. If each side of the pentagon measures $1 \mathrm{mm},$ and $\phi =\frac{\sqrt{5}+1}{2},$ find the area of pentagram in terms of $\phi .$

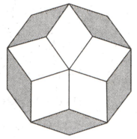
In the following diagram a regular decagon consists of $10$ parallelograms, out of which $5$ parallelograms that are meeting at the centre are congruent to each other and other $5$ parallelograms at the edges of the decagon are congruent to each other. If each side of the decagon is $1+\sqrt{5} \mathrm{cm},$ find total area of the $5$ parallelograms that are connected to the centre of the decagon.

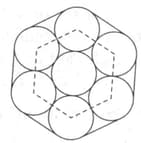
Take seven circles and close-pack them together in a hexagonal arrangement, as shown below. Then a rubber band is wrapped around the seven circles. Find the perimeter of this arrangement, if the radius of each circle is $\mathrm{r} \mathrm{cm}.$

In the given diagram, there are total seven regular hexagons. Let's call the outermost (or the largest) hexagon as ${\mathrm{H}}_1$ and so call the innermost (or the smallest) hexagon as ${\mathrm{H}}_7.$ The hexagon ${\mathrm{H}}_2$ is formed by joining the mid-points of the adjacent sides of ${\mathrm{H}}_1.$ Similarly, ${\mathrm{H}}_3, {\mathrm{H}}_4, {\mathrm{H}}_5, {\mathrm{H}}_6$ and ${\mathrm{H}}_7$ are formed by joining the mid-point of the adjacent sides of the ${\mathrm{H}}_2, {\mathrm{H}}_3,$ ${\mathrm{H}}_4,$ ${\mathrm{H}}_5$ and ${\mathrm{H}}_6,$ Respectively. If each side of the ${\mathrm{H}}_1$ is $64 \mathrm{cm},$ Find each side of the ${\mathrm{H}}_7.$