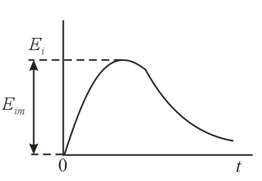
A flat coil with a cross-sectional area $S$ and with $N$ turns is placed in a magnetic field. The leads of the coil are connected to an oscillograph. When the coil is moved out of the field, an induction emf is generated in it, and the oscillograph of this emf is shown in the figure. How do the maximal value of the emf, $E_{1\mathrm{m}}$, and the area under the curve depending on the rate with which the coil is moved out of the field?

         

Suppose that we have two solenoids of the same length. Their diameters differ only to the extent to which one can be fitted onto the other. The inductances of the two solenoids can be considered the same and equal to $L$. Here are the ways in which the solenoids can be connected:

($1$) the solenoids are connected in series and are separated by a large distance;

($2$) the solenoids are connected in parallel and are separated by a large distance;

($3$) the solenoids are connected in series, one is fitted onto the other, and the senses of the turns coincide;

($4$) the solenoids are connected in parallel, one is fitted onto the other, and the senses of the turns coincide;

($5$) the solenoids are connected in series, one is fitted onto the other, and the senses of the turns are opposite;

($6$) the solenoids are connected in parallel, one is fitted onto the other, and the senses of the turns are opposite.

Determine the total inductance for each of the above cases.

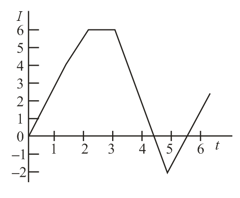
The current flowing in a certain inductance coil varies in time according to the curve shown schematically in the figure. Draw the curve representing the induced emf as a function of time (also schematically).

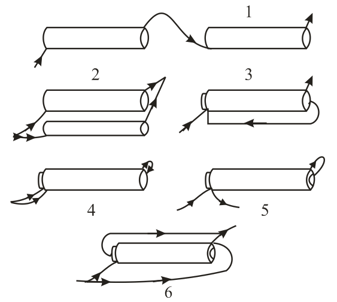
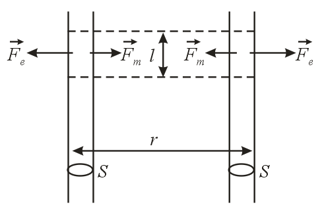
Two similar parallel electron beams point in the same direction. The linear dimensions of the cross section of each beam are small compared to the distance between the beams. Suppose that $v$ is the electron velocity and $n$ is the electron concentration in either beam. In a coordinate system with respect to which the electrons are in motion there are two types of interactions, the electrostatic and the magnetic. Which of the two is greater in magnitude?

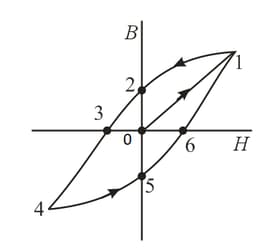
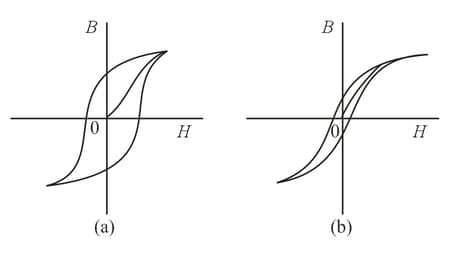
Two types of steel are characterized by the hysteresis loops shown in Figure. The loops are obtained in the processes of magnetization and demagnetization of the steels. Which of the two types is best suited for using as the core of a transformer and which, for using as a permanent magnet?

How can one use the $B$ vs. $H$ graph (the magnetization curve) to determine the work that a source of current must perform to magnetize a ferromagnetic core of a solenoid whose length is $l$ and whose cross-sectional area is $S$ ? The magnetization curve is shown in the figure accompanying the problem.

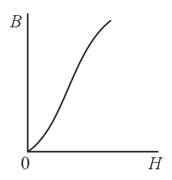
Does a hysteresis loop possess sections in which we can formally assign to permeability a value that is zero or infinite or negative?