A furniture firm manufactures chairs and tables, each requiring the use of three machines A, B and C. Production of one chair requires hours on machine A, hour on machine B and hour on machine C. Each table requires hour each on machine A and B and hours on machine C. The profit obtained by selling one chair is while by selling one table is . The total time available per week on machine A is hours, on machine B is hours and on machine C is hours. How many chairs and tables should be made per week so as to maximise the profit?
Formulate the problem as L.P.P. and solve it graphically.

Important Questions on Linear Programming
Suppose every gram of wheat provides g of proteins and g of carbohydrates, and the corresponding values for rice are g and g respectively. Wheat costs and rice per kilogram. The minimum daily requirement of an average man for proteins and carbohydrates is g and g respectively. In what quantities should wheat and rice be mixed in the daily diet to provide the minimum daily requirements of proteins and carbohydrates at minimum cost? What is the minimum cost?
To maintain one's health, a person must fulfil certain minimum daily requirements for the following three nutrients-calcium, protein and calories. His diet consists of only food items I and II whose prices and nutrient contents are shown below :
| Food I ₹ 6 per unit |
Food II ₹ 10 per unit |
Minimum daily requirement |
|
| Calcium | 10 | 4 | 20 |
| Protein | 5 | 5 | 20 |
| Calories | 2 | 6 | 12 |
Find the combination of food items so that the cost may be minimum.
Two godowns A and B have a grain storage capacity of quintals and quintals respectively. They supply to ration shops D, E and F, whose requirements are and quintals respectively. The costs of transportation per quintal from the godowns to the shops are given in the following table:
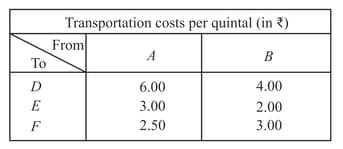
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
