Let A = θ ∈ R : 1 3 sin θ + 2 3 cos θ 2 = 1 3 sin 2 θ + 2 3 cos 2 θ . Then

A ∩ 0 , π has exactly one point

A ∩ 0 , π has exactly two points

A ∩ 0 , π has more than two points

MEDIUM

Earn 100

A group of $40$ students appeared in an examination of $3$ subjects - Mathematics, Physics & Chemistry. It was found that all students passed in at least one of the subjects, $20$ students passed in Mathematics, $25$ students passed in Physics, $16$ students passed in Chemistry, at most $11$ students passed in both Mathematics and Physics, at most $15$ students passed in both Physics and Chemistry, at most $15$ students passed in both Mathematics and Chemistry. The maximum number of students passed in all the three subjects is _____.

20.31% studentsanswered this correctly

Important Questions on Set Theory and Relations

MEDIUM

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

Consider the two sets:

A = {m \in R :

both the roots of

x^{2} - (m + 1) x + m + 4 = 0

are real

}

and

B = [- 3, 5)

Which of the following is not true?

MEDIUM

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

A survey shows that

63 %

of the people in a city read newspaper

A

whereas

76 %

read news paper

B

. If

x %

of the people read both the newspapers, then a possible value of

x

can be:

HARD

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

Let $\cup_{i = 1}^{50} X_{i} = \cup_{i = 1}^{n} Y_{i} = T$ , where each $X_{i}$ contains $10$ elements and each $Y_{i}$ contains $5$ elements. If each element of the set $T$ is an element of exactly $20$ of sets $X_{i}$ 's and exactly $6$ of sets $Y_{i}$ 's then $n$ is equal to :

HARD

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

Let

A = \{θ \in R : {(\frac{1}{3} \sin θ + \frac{2}{3} \cos θ)}^{2} = \frac{1}{3} \sin^{2} θ + \frac{2}{3} \cos^{2} θ\}

. Then

MEDIUM

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

In a class of

140

students numbered

1

140

, all even numbered students opted Mathematics course, those whose number is divisible by

3

opted Physics course and those whose number is divisible by

5

opted Chemistry course. Then the number of students who did not opt for any of the three courses is:

HARD

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

In a certain town,

25 %

families own a phone,

15 %

families own a car,

65 %

families own neither a phone nor a car and

2000

families own both a car and a phone. Consider the following Statements

(S) :

(S_{1}) :

35 %

families own at least one of a car or a phone.

(S_{2}) :

40, 000

families live in the town.
Then:

EASY

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

A survey shows that

73 %

of the persons working in an office like coffee, whereas

65 %

like tea. If

x

denotes the percentage of them, who like both coffee and tea, then

x

cannot be:

EASY

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

In a school, there are three types of games to be played. Some of the students play two types of games, but none play all the three games. Which Venn diagrams can justify the above statement?

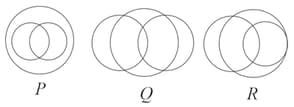
Question Image

MEDIUM

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

In a certain town,

25 %

of the families own a phone and

15 %

own a car;

65 %

families own neither a phone nor a car and

2000

families own both a car and a phone. Consider the following three statements:

(i)

5 %

families own both a car and a phone.

(i i)

35 %

families own either a car or a phone.

(i i i)

40000

families live in the town.

Then,

EASY

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

U

is the universal set with

100

elements;

A

and

B

are two sets such that

n (A) = 50, n (B) = 60

n (A \cap B) = 20

then

n (A^{'} \cap B^{'}) =

HARD

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

For any three sets

A, B

and

C

the set

(A \cup B \cup C) \cap {(A \cap B^{'} \cap C^{'})}^{'} \cap C^{'}

is equal to

EASY

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

A = {x | x \in N, x

is a prime number less than

12}

and

B = {x |

x \in N

x

is factor of

10}

, then

A \cap B

=

…

EASY

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

X

and

Y

are two sets, then

X \cap (Y \cup X)^{'}

equals

EASY

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

n (A) = 3, n (B) = 6

and

A \subseteq B,

then the number of elements in

(A \cup B)

is equal to

EASY

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

In a class of

175

students the following data shows the number of students opting one or more subjects. Mathematics

100

, Physics

70

, Chemistry

40

, Mathematics and Physics

30,

Mathematics and Chemistry

28

, Physics and Chemistry

23

, Mathematics, physics and Chemistry

18

. The number of students who have opted Mathematics alone is

EASY

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

n (P) = 8, n (Q) = 10

and

n (R) = 5

(

' n'

denotes cardinality) for three disjoint sets

P, Q, R

, then

n (P U Q U R) =

MEDIUM

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

A

and

B

are two non-empty sets, then

(B - A) \cap {(A \cap B)}^{'}

is equal to

EASY

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

A \subset B,

then

A Δ B

is equal to

MEDIUM

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

A = \{x \in R : |x| < 2\}

and

B = \{x \in R : |x - 2| \geq 3\};

then

MEDIUM

Mathematics>Algebra>Set Theory and Relations>Algebra of Sets

Two newspapers

A

and

B

are published in a city. It is known that

25 %

of the city population reads

A

and

20 %

reads

B

while

8 %

reads both

A

and

B .

Further,

30 %

of those who read

A

but not

B

look into advertisements and

40 %

of those who read

B

but not

A

also look into advertisements, while

50 %

of those who read both

A

and

B

look into advertisements. Then the percentage of the population who look into advertisements is:

Important Questions on Set Theory and Relations

Learn and Prepare for any exam you want !