A heavy particle is tied to the end $A$ of a string of length $1.6 \mathrm{m}$. Its other end $O$ is fixed. It revolves as a conical pendulum with the string making $60°$ with the vertical. Then,

A force of constant of magnitude $F$ acts on a particle (mass $m$) moving in a plane such that it is always perpendicular to the velocity $\overrightarrow{v}\left(\left|\overrightarrow{v}\right|=v\right)$ of the body. Select the correct option(s).

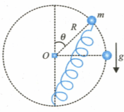
A bead of mass $m$ can slide without friction on a fixed vertical loop of radius $R$. The bead moves under the combined effect of gravity and a spring with spring constant $k$ only. The spring is rigidly attached to the bottom of the loop. Assume that the natural length of spring is zero. The bead is released from rest at $\mathrm{\theta }=0°$ with non-zero but negligible speed to the bead. The gravitational acceleration is directed downward as shown in the figure. Now choose the correct option(s). (Neglect any type of friction between any contact) (given $kR=mg/2$)

A weightless rod of length $2l$ carries two equal masses $m$. One is tied at end $A$ and other at middle of rod $B$. The rod can rotate in vertical plane about a fixed horizontal axis passing through $C$.

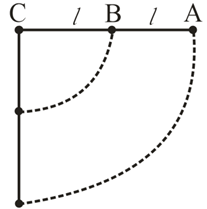
The rod is released from rest in horizontal position. Then, which of the following option(s) is/are correct?

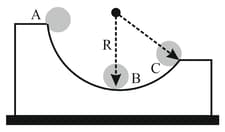
In the adjacent figure, a wedge of mass $2m$ is lying at rest on a horizontal surface. The wedge has a cavity which is the portion of a sphere of radius $R$. A small sphere of mass $m$ is released from the top edge of the cavity to slide down. All surfaces are smooth. Choose the correct option(s).

A bob of mass $2 \mathrm{kg}$ is suspended from point $O$ of a cone with an inextensible string of length $\sqrt{3} \mathrm{m}$. It is moving in horizontal circle over the surface of cone as shown in the figure. Then, which option(s) is(are) wrong $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$?

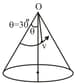
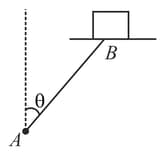
$A$ rod $AB$ of length $2 \mathrm{m}$ is hinged at point $A$ and its other end $B$ is attached to a platform on which a block of mass $m$ is kept. Rod rotates about point $A$ maintaining angle $\mathrm{\theta }=30°$ with the vertical in such a way that platform remains horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is $\mu =0.1$, then find the maximum angular velocity in $\mathrm{rad} {\mathrm{s}}^{-1}$ of rod so that the block does not slip on the platform, $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$