A helicopter flies horizontally with constant velocity in a direction east of north between two points and , at distance apart. Wind is blowing from south with constant speed , the speed of helicopter relative to air is , where . Find the speed of the helicopter along . The helicopter returns from to with same speed relative to air in same wind. Find the total time for the journeys.


Important Questions on Kinematics II
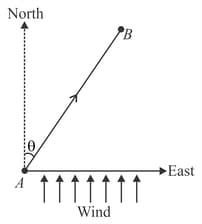
and are four trees, located at the vertices of a square. Wind blows from to with uniform speed. The ratio of times of flight of a bird from to and from to is . At what angle should the bird fly from the direction of wind flow, in order that it starts from and
(a) reaches ,
(b) reaches ?
Two particles are located on a horizontal plane at a distance . At both the particles are simultaneously projected at angle with velocities and , respectively.
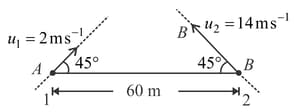
Find the minimum separation between them during motion.
At what time is the separation between them minimum?
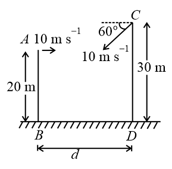
Two towers and are situated at distance apart as shown in figure. is high and is high from the ground. A particle is thrown from the top of horizontally with a velocity of towards . Simultaneously, another particle is thrown from the top of at an angle to the horizontal towards with the same magnitude of initial velocity as that of the first object. The two particles moving in the same vertical plane collide in mid-air. Calculate the distance between the towers.
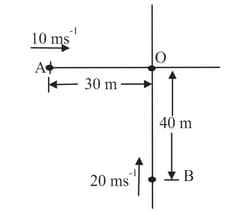
Two cars and are moving west to east and south to north, respectively, along crossroads. A moves with a speed of and is away from the point of intersection of cross roads and moves with a speed of and is away from the point of intersection of cross roads. Find the shortest distance between them.
Two particles and are moving with uniform velocity as shown in figure given below at .
(a) Will the two particles collide?
(b) Find out the shortest distance between two particles.
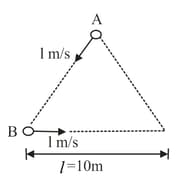
At , two particles and start moving with same speed along the sides of an equilateral triangle as shown in figure. Find the velocity of approach of
w.r.t. at time
(i) and
(ii)
A rocket moves horizontally with a constant velocity at a height . A guided missile is fired vertically with a speed when the rocket passes above it.

Assuming that the missile always aims at the rocket with the constant speed , find the time after the missile strikes the rocket.
