A hemispherical bowl of radius $r=0.1 \mathrm{m}$ is rotating about its axis (which is vertical) with an angular velocity $\omega$. A particle of mass ${10}^{-2} \mathrm{kg}$ on the frictionless inner surface of the bowl is also rotating with the same $\omega$. The particle is at a height $h$ from the bottom of the bowl. (a) Obtain the relation between $h$ and $\omega$. What is the minimum value of $\omega$ needed in order to have a nonzero value of $h$. (b) It is desired to measure $g$ using this setup by measuring $h$ accurately. Assuming that $r$ and $\omega$ are known precisely and that the least count in the measurement of $h$ is ${10}^{-4} \mathrm{m}$. What is minimum error $g$ in the measured value of $g$ $[g=9.8 \mathrm{m} {\mathrm{s}}^{-2}]$.

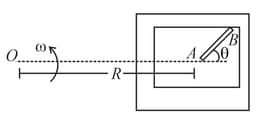
A table with the smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity $\omega$ in a circular path of radius $R$ (figure). A smooth groove $AB$ of length $L(\ll R)$ is made on the surface of the table. The groove makes an angle $\theta$ with the radius $OA$ of the circle in which the cabin rotates. A small particle is kept at the point $A$ in the groove and is released to move along $AB$. Find the time taken by the particle to reach the point $B$.

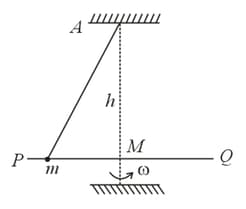
A smooth rod $PQ$ is rotated in a horizontal plane about its mid-point $M$ with height, $h=0.1 \mathrm{m}$ vertically below a fixed point $A$ at a constant angular velocity $14 \mathrm{rad} {\mathrm{s}}^{-1}$. A light elastic string of natural length $0.1 \mathrm{m}$ requiring $1.47 \mathrm{N} {\mathrm{cm}}^{-1}$ has one end fixed at $A$ and its other end attached to a ring of mass $m=0.3 \mathrm{kg}$ which is free to slide along the rod. When the ring is stationary relative to the rod, then find inclination of string with vertical, tension in string and force exerted by the ring on the rod $(g=9.8 \mathrm{m} {\mathrm{s}}^{-2})$.

A mass $m_1$ lies on fixed smooth cylinder. An ideal cord attached to $m_1$ passes over the cylinder and is connected to mass $m_2$ as shown in the figure.

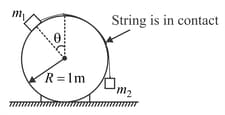
 Find the value of $\mathrm{\theta }$ in degree (shown in the diagram) for which the system is in equilibrium if $m_1=\sqrt{2} \mathrm{kg}$ and $m_2=1 \mathrm{kg}$.

A mass $m_1$ lies on fixed smooth cylinder. An ideal cord attached to $m_1$ passes over the cylinder and is connected to mass $m_2$ as shown in the figure.

 if $m_1=5 \mathrm{kg}, m_2=4 \mathrm{kg}$. The system is released from rest when $\mathrm{\theta }=30°$. Find the value of $N$ if the magnitude of the acceleration of mass $m_1$ just after the system is released is $\frac{N}{9} \mathrm{m} {\mathrm{s}}^{-2}$.

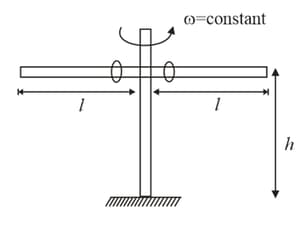
Two identical rings which can slide along the rod are kept near the midpoint of a smooth rod of length $2l(l=1 \mathrm{m})$ The rod is rotated with constant angular velocity $\omega =3 \mathrm{rad} {\mathrm{s}}^{-1}$ about the vertical axis passing through its center. The rod is at height $h=5 \mathrm{m}$ from the ground. Find the distance (in meter) between the points on the ground where the rings will fall after leaving the rods.

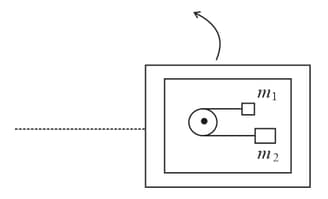
A table with the smooth horizontal surface is placed in a cabin which moves in a circle of a large radius $R$ (figure). A smooth pulley of a small radius is fastened to the table. Two masses $m$ and $2m$ placed on the table are connected through a string over the pulley. Initially, the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the value of $\frac{T}{ma}$, where $a$ is the magnitude of the initial acceleration of the masses as seen from the cabin and $T$ is the tension in the string.

A uniform square plate of mass m is supported as shown. If the cable suddenly breaks, determine just after that moment 

(a) The angular acceleration of the plate. 

(b) The acceleration of corner $C$.   

(c) The reaction at $A$.