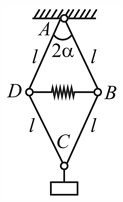
A hexagonal pencil placed on an in lined plane with a slope at right angle the generatrix (i.e. the line of intersection of the plane and the horizontal surface remains at rest. The same pencil place parallel to the generatrix rolls down th lane.
Determine the angle between the axis of the pencil and the generatrix of the inclined plane (Fig.) at which the pencil is still in equilibrium.
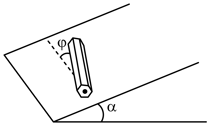
Determine the angle between the axis of the pencil and the generatrix of the inclined plane (Fig.) at which the pencil is still in equilibrium.


Important Questions on Mechanics
A homogeneous rod of length leans against a vertical wall at one end and against a smooth stationary surface at another end.
What function must be used to describe the cross section of this surface for the rod to remain in equilibrium in any position even in the absence of friction? Assume that the rod remains all the time in the same vertical plane perpendicular to the plane of the wall.
A thin perfectly rigid weightless rod with a point-like ball fixed at one end is deflected through a small angle from its
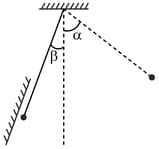
equilibrium position and then released. At the moment when the rod forms an angle $\beta<\alpha$ with the vertical, the ball undergoes a perfectly elastic collision with an inclined wall (Fig).
Determine the ratio of the period of oscillations of this pendulum to the period of oscillations of a simple pendulum having the same length.
A ball of mass falls from a certain height on the pan of mass of a spring balance. The rigidity of the sprin is .
Determine the displacement of the point about which the pointer of the balance will oscillate, assuming that the collisions of the ball with the pan are perfectly elastic.
Prove that there exists a point at which the condition of harmonicity of oscillations will be violated.
Two blocks having mass and and connected by a spring of rigidity lie on a horizontal plane.
Determine the period of small longitudinal oscillations of the system, neglecting friction.
A heavy round log is suspended at the ends on two ropes so that the distance between the points of suspension of the ropes is equal to the diameter of the log. The length of each vertical segment of the ropes is .
Determine the period of small oscillations of the system in a vertical plane perpendicular to the log.
A load of mass is on horizontal rails. A pendulum made of a ball of mass tied to a weightless inextensible thread is suspended to the load. The load can move only along the rails.
Determine the ratio of the periods of small oscillations of the pendulum in vertical planes parallel and perpendicular to the rails.
Determine the period of small oscillations of the load.