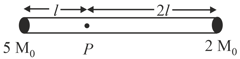
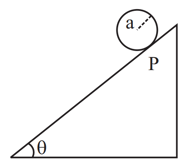
A hollow hemispherical bowl having radius of inner smooth surface$\mathrm{R}=80 \mathrm{cm}$ is rotated with angular velocity = $5 \mathrm{rad} {\mathrm{s}}^{-1}$. A small object is placed at rest w.r.t. the bowl of position as shown. Find angle $\theta$.

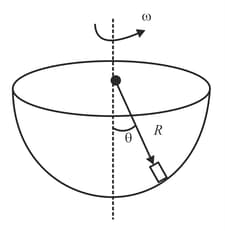
A solid sphere rolls without slipping, first horizontally and then up to a point $x$ at height $h$ on an inclined plane before rolling down, as shown in the figure below.

The initial horizontal speed of the sphere is

One end of a rod of length $L=1 \mathrm{m}$ is fixed to a point on the circumference of a wheel of radius $R=\frac{1}{\sqrt{3}} \mathrm{m}.$ The other end is sliding freely along a straight channel passing through the center $O$ of the wheel as shown in the figure below. The wheel is rotating with a constant angular velocity $\omega$ (in radian per second) about $O.$

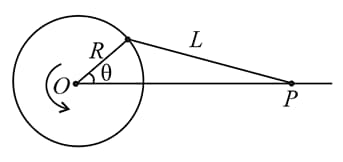
The speed of the sliding end $P$ when $\theta =60°$ is

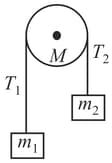
On a pulley of mass $M$ hangs a rope with two masses $m_1$ and $m_2\left(m_1>m_2\right)$ tied at the ends as shown in the figure. The pulley rotates without any friction, whereas the friction between the rope and the pulley is large enough to prevent any slipping. Which of the following plots best represents the difference between the tensions in the rope on the two sides of the pulley as a function of the mass of the pulley?

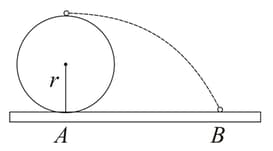
A rigid ball rolls without slipping on a surface shown below.

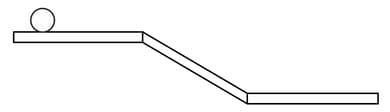
Which on the following is the most likely representation of the distance travelled by the ball vs time graph?

The angular speed of truck wheel is increased from $900 \mathrm{rpm}$ to $2460 \mathrm{rpm}$ in $26$ seconds. The number of revolutions by the truck engine during this time is ______.

(Assuming the acceleration to be uniform).

A solid disc of radius $a$ and mass $m$ rolls down without slipping on an inclined plane making an angle $\theta$ with the horizontal. The acceleration of the disc will be $\frac{2}{\mathit{ }b}g\sin \theta$, where $b$ is _______.  (Round off to the nearest integer)

($g=$ acceleration due to gravity and $\theta =$ angle as shown in figure)

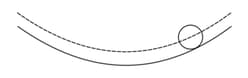
A ball is rolling without slipping in a spherical shallow bowl (radius $R$ ) as shown in the figure and is executing simple harmonic motion. If the radius of the ball is doubled, then the time period of oscillation

A wheel of radius "rolls without slipping with a speed $v$ on a horizontal road. When it is at a point $A$ on the road a small bob of the mud separates from wheel at the highest point and touches the point $B$ on the road as shown in the figure. Then $AB$ is (g-acceleration due to gravity)

A rigid massless rod of length $3l$ has two masses attached at each end as shown in the figure. The rod is pivoted at point $P$ on the horizontal axis. When released from the initial horizontal position, its instantaneous angular acceleration will be