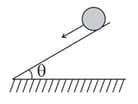
A hollow sphere is set into motion on a rough horizontal surface with a speed $v$ in the forward direction and a rotational speed $v/R$ in the anticlockwise direction as shown in the figure. Find the translational speed of the sphere $\left(\mathrm{a}\right)$ when it stops rotating and $\left(\mathrm{b}\right)$ when slipping finally ceases and pure rolling starts.

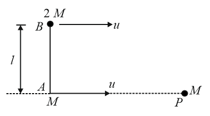
Two small particles $A \text{and} B$ of masses $M \text{and }2M$ respectively, are joined rigidly to the ends of a light rod of length $l$ as shown in the figure. The system translates on a smooth horizontal surface with a velocity $u$ in a direction perpendicular to the rod. A particle $P$ of mass $M$ kept at rest on the surface sticks to the particle $A$ as the particle $P$ collides with it. Then choose the correct option(s) 

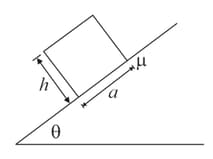
A block with a square base measuring $a\times a$ and height $h$, is placed on an inclined plane. The coefficient of friction is $\mu$. The angle of inclination $\left(\theta \right)$ of the plane is gradually increased. The block will:

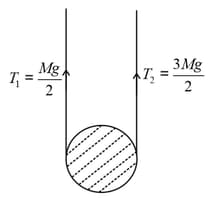
A uniform disc of mass $M$ and radius $R$ is lifted using a string as shown in the figure. Then,

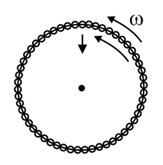
A circular loop of rope of length $\mathrm{L}$ rotates with uniform angular velocity $\mathrm{\omega }$ about an axis through its centre on a horizontal smooth platform.Velocity of pulse (with respect to rope ) produce due to slight radial displacement is given by$\left(\frac{\omega L}{2\mathrm{\pi }}\right)$, If the motion of the pulse and rotation of the loop, both are in same direction then the velocity of the pulse w.r.t. to ground will be:

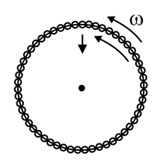
A circular loop of rope of length $L$ rotates with uniform angular velocity $\omega$ about an axis through its centre on a horizontal smooth platform. Velocity of pulse (with respect to rope ) produce due to slight radial displacement is given by$\left(\frac{\omega L}{2\mathrm{\pi }}\right)$, If both are in opposite directions, then the velocity of the pulse with respect to the ground will be:

The potential energy of a particle of mass $m$ at a distance $r$ from a fixed point $O$ is given by $V\left(r\right)=k{r}^2/2$, where $k$ is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius $R$ about the point $O$. If $v$ is the speed of the particle and $L$ is the magnitude of its angular momentum about $O$, which of the following statements is (are) true?

A solid sphere of radius $R$ has a moment of inertia $I$ about its geometrical axis. If it is melted into a disc of radius $r$ and thickness $t$. If it's moment of inertia about the tangential axis (which is perpendicular to the plane of the disc), is also equal to $I$, then the value of $r$ is equal to

A solid sphere is in pure rolling motion on an inclined surface having inclination $\mathrm{\theta }$, the friction force acting on sphere will be,