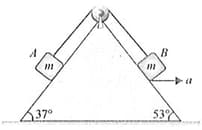
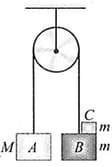
A homogeneous flexible rope rests on a wedge whose side edges make angles $\alpha$ and $\beta$ with the horizontal (refer figure). The central part of the rope lies on the upper rib $C$ of the wedge. [Consider all surfaces to be smooth] With what acceleration should the wedge be pulled to the left along the horizontal plane in order to prevent the displacement of the rope with respect to the wedge?

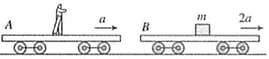
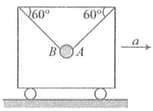
Two trolleys $\mathrm{A}$ and $\mathrm{B}$ are moving with accelerations $\mathrm{a}$ and $2\mathrm{a}$, respectively, in the same direction. To an observer in trolley $\mathrm{A}$, Find the magnitude of the pseudo force acting on a block of mass $\mathrm{m}$ on trolley $\mathrm{B}$.

Two blocks $A$ and $B$ of equal masses $m \mathrm{kg}$ each are connected by a light thread which passes over a massless pulley as shown. Both the blocks lie on wedge of mass $m$. Assume friction to be absent everywhere and both the blocks to be always in contact with the wedge. The wedge lying over smooth horizontal surface is pulled towards right with constant acceleration $a$ ($g$ is acceleration due to gravity).

(i) Find the normal reaction acting on block $A$.

(ii) Find the normal reaction acting on block $B$.

(iii) Find the accelerations of block $A$ and block $B$ with respect to wedge.

(iv) Find the maximum value of acceleration $a$ for which normal reactions acting on the block $A$ and block $B$ are non-zero.

Assuming that the magnitudes of the acceleration and the acceleration are the same, a person is standing on a weighing machine placed on the floor of an elevator. The elevator starts going up with some acceleration, moves with uniform velocity for a while and finally decelerates to stop. The maximum and the minimum weights recorded are $72 \mathrm{kg}$ and $60 \mathrm{kg}$, find

(a) the true weight of the person and

(b) the magnitude of the acceleration. 

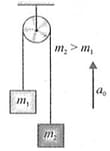
In the given figure, the pulley and strings are light. The pulley is suspended in a elevator moving up with acceleration $a_0$. Find the accelerations of the blocks with respect to elevator.

In the given system, the pulley is light and frictionless; string is also massless. Initially the system is in equilibrium. Now a small block $C$ of mass $m$ is placed on the block $B$ of mass $M$. If block $C$ always remains on block $B$, find the normal reaction on $C$ due to $B$.

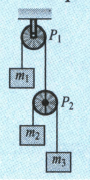
In the arrangement of three blocks as shown in the figure, the string is inextensible. If the directions of accelerations are as shown in the figure, then determine the constraint relation.

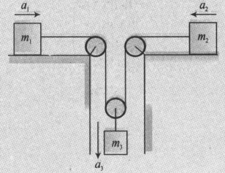
A pulley-rope-mass arrangement is shown in the figure. Find the acceleration of block $m_1$ when the masses are set free to move. Assume that the pulley and the ropes are ideal.