A jar is filled with two non-mixing liquids $1$ and $2$ having densities ${\mathrm{\rho }}_1$ and ${\rho }_2$ respectively. A solid ball, made of a material of density ${\mathrm{\rho }}_3,$ is dropped in the jar. It comes to equilibrium in the position shown in the figure.

 

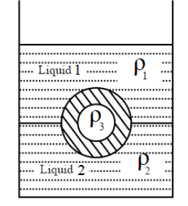
Which of the following is true for ${\mathrm{\rho }}_1, {\mathrm{\rho }}_2$ and ${\rho }_3$?

An open glass tube is immersed in mercury in such a way that a length of $8 \mathrm{cm}$ extends above the mercury level. The open-end of the tube is then closed and sealed and the tube is raised vertically up by an additional$46 \mathrm{cm}$. What will be length of the air column above mercury in the tube now? (Atmospheric pressure$=76 \mathrm{cm} \text{of} \mathrm{Hg}$)

A ball of density d is dropped onto a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time t1. Next, the ball is released and it falls through the same height before striking the surface of a liquid of density${\mathrm{d}}_{\mathrm{L}}.$

$\left(\mathrm{a}\right)$ If $\mathrm{d} < {\mathrm{d}}_{\mathrm{L}},$ obtain an expression $(\mathrm{in} \mathrm{terms} \mathrm{of} \mathrm{d} , {\mathrm{t}}_1 \mathrm{and} {\mathrm{d}}_{\mathrm{L}})$ for the time ${\mathrm{t}}_2$ the ball takes to come back to the position from which it was released.

$\left(\mathrm{b}\right)$ Is the motion of the ball simple harmonic?

$\left(\mathrm{c}\right)$ If $\mathrm{d} = {\mathrm{d}}_{\mathrm{L}},$ how does the speed of the ball depend on its depth inside the liquid ?
     Neglect all frictional and other dissipative forces. Assume the depth of the liquid to be large.

A container of large uniform cross-sectional area $A$ resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities $d$ and $2d$, each of height $\frac{H}{2}$ as shown in the figure. The lower density liquid is open to the atmosphere having pressure $P_0$.

$\left(\mathrm{a}\right)$ A homogeneous solid cylinder of length $L$, $\left(L<\frac{H}{2}\right)$ cross-sectional area $\frac{A}{5}$ is immersed such that it floats with its axis vertical at the liquid-liquid interface with the length $\frac{L}{4}$ in the denser liquid. Determine:

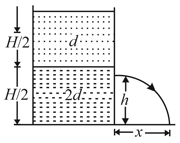
$\left(\mathrm{i}\right)$ The density $D$ of the solid and $\left(\mathrm{ii}\right)$ The total pressure at the bottom of the container.

$\left(\mathrm{b}\right)$ The cylinder is removed and the original arrangement is restored. A tiny hole in the area $s\left(s<<A\right)$ is punched on the vertical side of the container at a height $h$, $\left(h<\left(\frac{H}{2}\right)\right)$. Determine: 

$\left(\mathrm{i}\right)$ The initial speed of efflux of the liquid at the hole.

$\left(\mathrm{ii}\right)$ The horizontal distance $x$ travelled by the liquid initially and

$\left(\mathrm{iii}\right)$ The height hm at which the hole should be punched so that the liquid travels the maximum distance $x_{\mathrm{m}}$ initially. Also, calculate $x_{\mathrm{m}}$.