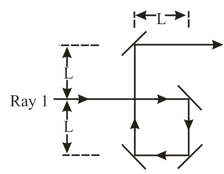
A light wave along ray $r_1$ reflects once from a mirror, and a light wave along ray $r_2$ reflects twice from that same mirror and once from a tiny mirror at distance $L$ from the bigger mirror. (Neglect the slight tilt of the rays.) The waves have wavelength $\mathrm{\lambda }$ and are initially exactly out of phase. What are the smallest, second smallest and fourth smallest values of $\frac{L}{\mathrm{\lambda }}$, that result in the final waves being exactly in phase?

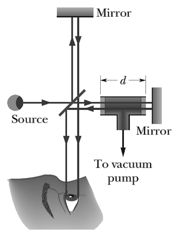
In the following figure, an airtight chamber of length $d=5.0 \mathrm{cm}$ is placed in one of the arms of a Michelson interferometer. (The glass window on each end of the chamber has negligible thickness.) Light of wavelength $\mathrm{\lambda }=500 \mathrm{nm}$ is used. Evacuating the air from the chamber causes a shift of $60$ bright fringes. From this data and to six significant figures, find the index of refraction of air at the atmospheric pressure.

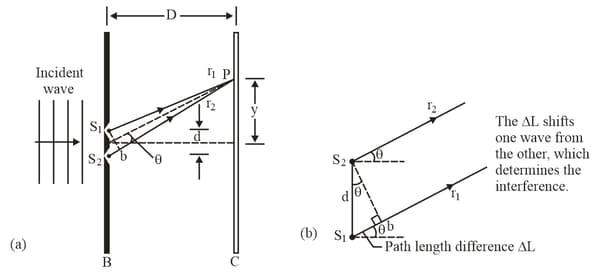
In the double-slit experiment, as shown in the following figure, the viewing screen is at distance $D=4.00 \mathrm{m}$. Point $p$ lies at distance $y=20.5 \mathrm{cm}$ from the centre of the pattern, the slit separation $d$ is $4.50 \mathrm{\mu m}$, and the wavelength $\mathrm{\lambda }$ is $650 \mathrm{nm}$.

(a) Determine where point $P$ is in the interference pattern by giving the maximum or minimum on which it lies, or the maximum and minimum between which it lies.

(b) What is the ratio of the intensity $I_{\mathrm{P}}$ at point $P$ to the intensity $I_{\mathrm{cen}}$ at the centre of the pattern?

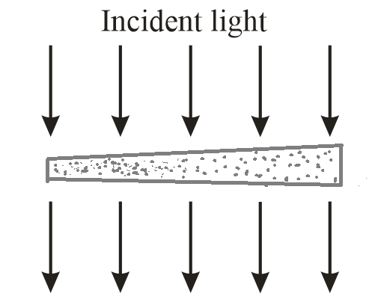
In the below figure, a broad beam of light of wavelength $420 \mathrm{nm}$ is incident at $90°$ on a thin, wedge-shaped film with an index of refraction $1.70$. The transmission gives $10$ bright and $9$ dark fringes along the film's length. What is the left-to-right change in the film thickness?

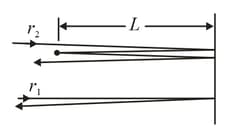
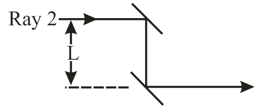
In the below figure, two light rays go through different paths by reflecting from the various flat surfaces shown. The light waves have a wavelength of $411.0 \mathrm{nm}$ and are initially in phase. What is the smallest and the second smallest value of distance $L$ that will put the waves exactly out of phase as they emerge from the region?

In the following figure, assume that the two light waves, of wavelength $515 \mathrm{nm}$ in the air, are initially out of phase by $\mathrm{\pi } \mathrm{rad}$. The indexes of refraction of the media are $n_1=1.45$ and $n_2=1.75$. What is the smallest and second smallest value of $L$ that will put the waves exactly in phase, once they pass through the two media?

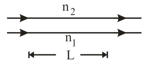
In a double-slit experiment, the fourth-order maximum for a wavelength of $450 \mathrm{nm}$ occurs at an angle of $\mathrm{\theta }=90°$.

(a) What range of wavelengths in the visible range $(400 \mathrm{nm}$ to $700 \mathrm{nm})$ is not present in the third-order maxima?

(b) To eliminate all the visible light in the fourth-order maximum, should the slit separation be increased or decreased and (c) What least change is needed?