A linear harmonic oscillator has a total mechanical energy of $200\mathrm{J}$. Potential energy of it at mean position is $50\mathrm{J}$. Find

(i) The maximum kinetic energy

(ii) The minimum potential energy

(iii) The potential energy at extreme positions.

The potential energy of a particle oscillating on $x-$axis is given as $U=20+{\left(x-2\right)}^2$.

Here $U$ is in joules and $x$ in metres. Total mechanical energy of the particle is $36\mathrm{J}$.

(a) State whether the motion of the particle is simple harmonic or not.

(b) Find the mean positive

(c) Find the maximum kinetic energy of the particle.

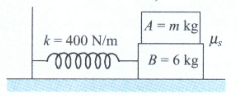
A block of mass $m$ is suspended from the ceiling of a stationary elevator through a spring of spring constant $k$; it is in equilibrium. Suddenly, the cable breaks and the elevator starts falling freely. Show that the block now executes a simple harmonic motion of amplitude $\frac{mg}{k}$ in the elevator.

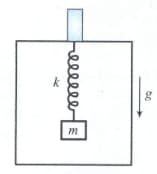
A ball of mass $m$ is connected to two rubber bands of length $L$, each under tension $T$ as shown in the figure. The ball is displaced by a small distance $y$ perpendicular to the length of the rubber bands. Assuming the tension does not change, show that

(a) the restoring force is $-\left(\frac{2\mathrm{T}}{L}\right)y$ and

(b) the system exhibits simple harmonic motion with an angular frequency $\omega =\sqrt{\frac{2\mathrm{T}}{mL}}$.

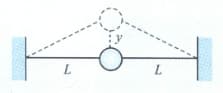
Two blocks lie on each other and are connected to a spring as shown in the figure. What should be the mass of block $A$ placed on block $B$ of mass $6\mathrm{kg}$ so that the system is period is $1\mathrm{s}$. Assuming no slipping, what should be the minimum value of coefficient of static friction $\mu$, for which block $A$ will not slip relative to block $B$, if block $B$ is displaced $50\mathrm{mm}$ from equilibrium position and released?

(Given: $g=10{\mathrm{ms}}^{-2}$ and ${\pi }^2=10$)