A uniform solid sphere rolls down a vertical surface without sliding. If the vertical surface moves with an acceleration a = g 2 , find the minimum coefficient of friction between the sphere and vertical surfaces so as to prevent relative sliding.

We have to find out the minimum coefficient of friction between the sphere and vertical surfaces to prevent relative sliding motion. In the diagram α is angular acceleration in a clockwise direction. Now if we consider horizontal equilibrium then Normal force N = m g 2 . . . ( 1 ) And for vertical motion equation would be m g - f = m a ' . . . ( 2 ) And torque equation would be f × R = 2 5 m R 2 × α . . . ( 3 ) Pure rolling is given by a ' = α R so ( 3 ) becomes f × R = 2 5 m a ' R friction f = 2 5 m a ' . . . ( 4 ) so ( 2 ) becomes m g - 2 5 m a ' = m a ' m g = 2 5 + 1 m a ' m g = 7 5 m a ' a ' = 5 7 g so ( 4 ) becomes f = 2 5 × m × 5 7 × g f = 2 7 m g So the coefficient of friction is the ratio of the friction force resisting the motion of two surfaces in contact to the normal force pressing the two surfaces together. μ = F N Where F is the frictional force and N is the normal force. μ = 2 7 m g × 2 m g μ = 4 7 This is the expression for coefficient of friction for no slipping.

A rod of mass m spins with an angular speed ω = g / l , Find its (a) kinetic energy of rotation. (b) kinetic energy of translation (c) total kinetic energy.

(a) Kinetic energy of rotation can be calculated by formula K rotational = 1 2 I C ω 2 where I C is the moment of inertia of centre of mass which is equal to m l 2 12 for the rod and ω is the angular speed of rotation. ⇒ K rotational = 1 2 m l 2 12 g l 2 ⇒ K r o t a t i o n a l = 1 24 m g l (b) Kinetic energy of translation can be calculated by formula K translational = 1 2 m v c 2 where v c is the velocity of centre of mass of rod which can be calculated by formula v c = ω l 2 . ⇒ K translational = 1 2 m ω l 2 2 ⇒ K translational = 1 2 m g l × l 2 2 ⇒ K translational = 1 8 m g l (c) We know that total kinetic energy is equal to translational kinetic energy and rotational kinetic energy. Hence, we can write K total = K translational + K rotational ⇒ K total = 1 2 I P ω 2 + 1 2 m l 2 3 g l 2 ⇒ K t o t a l = 1 6 m g l

MEDIUM

JEE Advanced

IMPORTANT

Earn 100

A load of mass $m$ is attached to the end of a string wound on a cylinder of mass $M$ and radius $R$ . The string passes round a pulley.

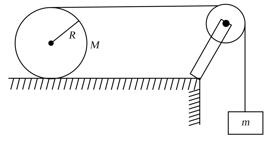
(a) Find the acceleration of the cylinder $M$ when it rolls.
(b) If the coefficient of friction is $μ$ . Find the acceleration of the cylinder when it slips and rolls.
(c) Find the minimum value of coefficient of friction for which the cylinder rolls always.

Important Questions on Rigid Body Dynamics: Part 2

HARD

JEE Advanced

IMPORTANT

Physics For Joint Entrance Examination JEE (Advanced): Mechanics II>Chapter 4 - Rigid Body Dynamics: Part 2>CONCEPT APPLICATION EXERCISE>Q 3

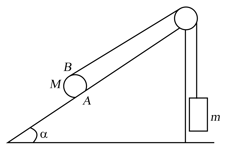
Find the tension in the tape and the linear acceleration of the cylinder up the incline, assuming there is no slipping. (Take $M = 4 m$ and $g = 10 m s^{- 2}$ )
Question Image

HARD

JEE Advanced

IMPORTANT

Physics For Joint Entrance Examination JEE (Advanced): Mechanics II>Chapter 4 - Rigid Body Dynamics: Part 2>CONCEPT APPLICATION EXERCISE>Q 4

A uniform solid sphere rolls down a vertical surface without sliding. If the vertical surface moves with an acceleration $a = \frac{g}{2}$ , find the minimum coefficient of friction between the sphere and vertical surfaces so as to prevent relative sliding.
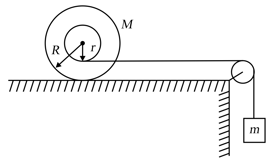
Question Image

MEDIUM

JEE Advanced

IMPORTANT

Physics For Joint Entrance Examination JEE (Advanced): Mechanics II>Chapter 4 - Rigid Body Dynamics: Part 2>CONCEPT APPLICATION EXERCISE>Q 5

A spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown in figure. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass m is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is $a_{C M} \neq α R$ and radius is $R$ . Find the acceleration of the falling mass $m$ . Neglect the mass of the connecting tube and slipping of the spool.
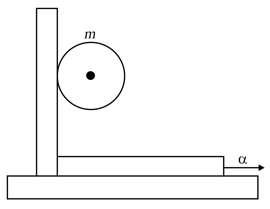
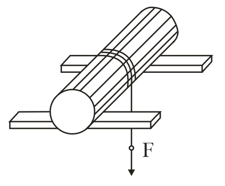
Question Image

MEDIUM

JEE Advanced

IMPORTANT

Physics For Joint Entrance Examination JEE (Advanced): Mechanics II>Chapter 4 - Rigid Body Dynamics: Part 2>CONCEPT APPLICATION EXERCISE>Q 6

A solid cylinder wheel of mass

M

and radius

R

is pulled by a force

F

applied to the centre of the wheel at

37 °

to the horizontal. If the wheel is to roll without slipping, what is the maximum value of

|F|

? The coefficients of static and kinetic friction are

μ_{S} = 0.40

and

μ_{K} = 0.30 . (\sin 37 ° = \frac{3}{5})

HARD

JEE Advanced

IMPORTANT

Physics For Joint Entrance Examination JEE (Advanced): Mechanics II>Chapter 4 - Rigid Body Dynamics: Part 2>CONCEPT APPLICATION EXERCISE>Q 7

A uniform solid cylinder of mass $m$ , rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down, with a constant force $F$ . Find the maximum magnitude of the force $F$ , which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to $k$ . What is the acceleration $ω_{\max}$ , of the axis of the cylinder, rolling down the inclined plane?

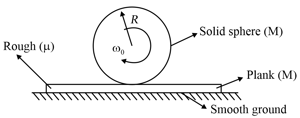
Question Image

MEDIUM

JEE Advanced

IMPORTANT

Physics For Joint Entrance Examination JEE (Advanced): Mechanics II>Chapter 4 - Rigid Body Dynamics: Part 2>CONCEPT APPLICATION EXERCISE>Q 9

A solid sphere of mass $M$ is placed on the top of a plank of the same mass, after giving an angular velocity $ω_{0}$ at $t = 0$ . Find the velocity of the plank and the sphere when the sphere starts rolling.
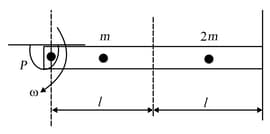
Question Image

EASY

JEE Advanced

IMPORTANT

Physics For Joint Entrance Examination JEE (Advanced): Mechanics II>Chapter 4 - Rigid Body Dynamics: Part 2>CONCEPT APPLICATION EXERCISE>Q 1

A rod of mass $m$ spins with an angular speed $ω = \sqrt{g / l}$ , Find its
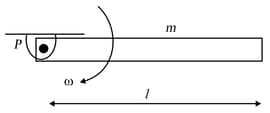
Question Image
(a) kinetic energy of rotation.
(b) kinetic energy of translation
(c) total kinetic energy.

HARD

JEE Advanced

IMPORTANT

Physics For Joint Entrance Examination JEE (Advanced): Mechanics II>Chapter 4 - Rigid Body Dynamics: Part 2>CONCEPT APPLICATION EXERCISE>Q 2

Find $K E$ of the rotating composite rod comprising two rods of mass $m$ and $2 m$ and each of length $l = 1 m$ . Assume $ω = 10$ rad $s^{- 1}$ and $m = 1 k g$ .
Question Image

Important Questions on Rigid Body Dynamics: Part 2

Learn and Prepare for any exam you want !