A loop-the-loop machine has a radius of $18\mathrm{m}$.

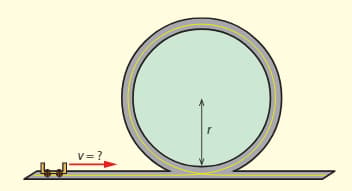
a. Calculate the minimum speed with which a cart must enter the loop so that it does not fall off at the highest point.

A loop-the-loop machine has a radius of $18\mathrm{m}$.

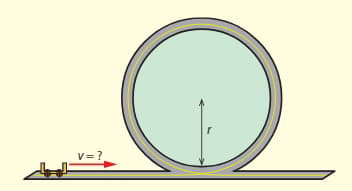
b. Predict the speed at the top in this case.

The diagram shows a horizontal disc with a hole through its centre. A string passes through the hole and connects a mass $m$ on top of the disc to a bigger mass $M$ that hangs below the disc. Initially, the smaller mass is rotating on the disc in a circle of radius $r$. Determine the speed of $m$  be such that the big mass stands still.

,

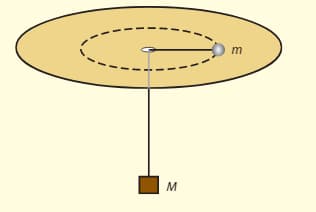
The ball shown in the diagram is attached to a rotating pole with two strings. The ball has a mass of $0.250\mathrm{kg}$ and rotates in a horizontal circle at a speed of $8.0 \mathrm{m}/\mathrm{s}$.

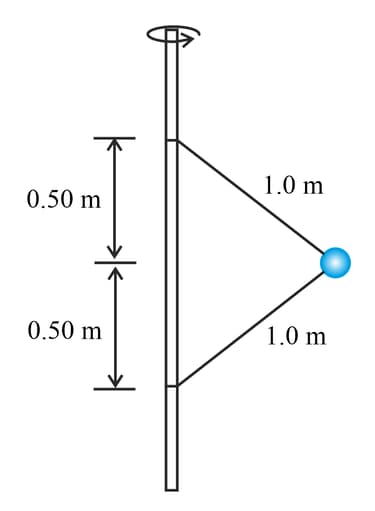
Determine the tension in each string.

In an amusement park ride a cart of mass $300\mathrm{kg}$ and carrying four passengers each of mass $60\mathrm{kg}$ is dropped from a vertical height of $120\mathrm{m}$ along a frictionless path that leads into a loop-the-loop machine of radius $30\mathrm{m}$. The cart then enters a straight stretch from A to C, where friction brings it to rest after a distance of $40\mathrm{m}$.

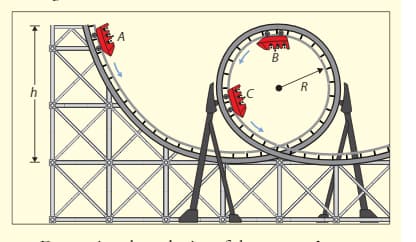
a. Determine the velocity of the cart at A.

In an amusement park ride a cart of mass $300\mathrm{kg}$ and carrying four passengers each of mass $60\mathrm{kg}$ is dropped from a vertical height of $120\mathrm{m}$ along a frictionless path that leads into a loop-the-loop machine of radius $30\mathrm{m}$. The cart then enters a straight stretch from A to C, where friction brings it to rest after a distance of $40\mathrm{m}$.

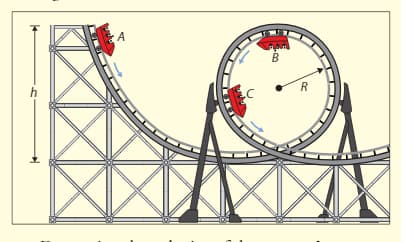
b. Calculate the reaction force from the seat the cart onto the passenger at B.

In an amusement park ride a cart of mass $300\mathrm{kg}$ and carrying four passengers each of mass $60\mathrm{kg}$ is dropped from a vertical height of $120\mathrm{m}$ along a frictionless path that leads into a loop-the-loop machine of radius $30\mathrm{m}$. The cart then enters a straight stretch from A to C, where friction brings it to rest after a distance of $40\mathrm{m}$.

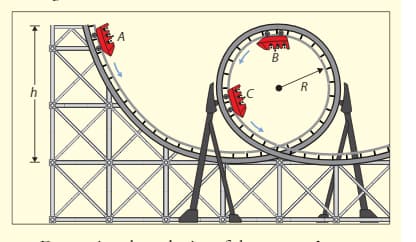
c. Determine the acceleration experienced by the cart from A to C.