A pair of charged parallel plates are arranged horizontally in a vacuum. The upper plate carries a negative charge and the lower plate is earthed.
An electron enters the space between the plates at right angles to the electric field. In which direction is the electric field between the plates and in which direction is the force on the electron?
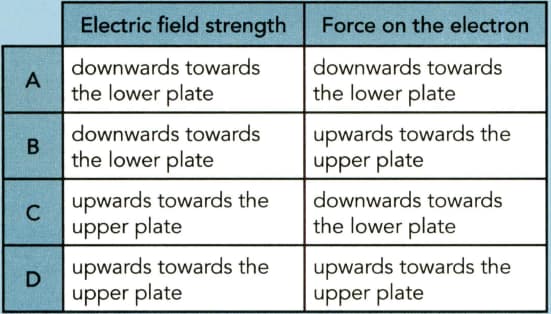
An electron enters the space between the plates at right angles to the electric field. In which direction is the electric field between the plates and in which direction is the force on the electron?


Important Questions on Uniform Electric Fields
A pair of charged parallel plates are $2.0 \mathrm{~cm}$ apart and there is a potential difference of $5.0 \mathrm{kV}$ across the plates. A charged ion between the plates experiences a force of $1.2 \times 10^{-13} \mathrm{~N}$ due to the field. What is the charge on the ion?
(a)
(b)
(c)
(d)
Figure shows apparatus used to investigate the field between a pair of charged, parallel plates.
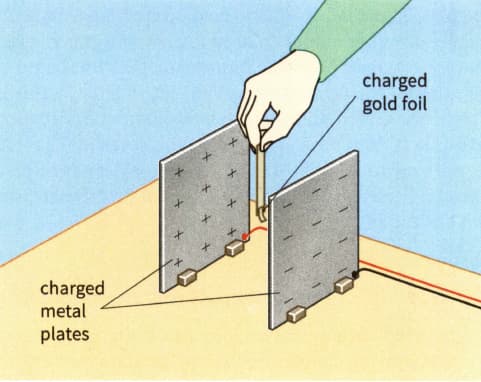
Investigating the electric field between two charged metal plates.
Explain why the piece of gold foil deflects in the manner shown.
Figure shows apparatus used to investigate the field between a pair of charged, parallel plates.
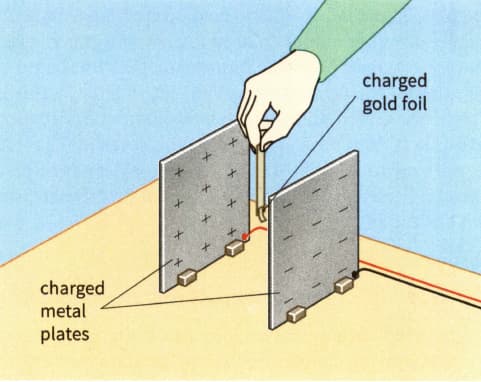
Investigating the electric field between two charged metal plates.
State and explain what would be observed if the gold foil momentarily touched the negatively charged plate.
A charged dust particle in an electric field experiences a force of $4.4 \times 10^{-13} \mathrm{~N}$. The charge on the particle is $8.8 \times 10^{-17} \mathrm{C}$. Calculate the electric field strength.
A potential difference of $2.4 \mathrm{kV}$ is applied across a pair of parallel plates. The electric field strength between the plates is $3.0 \times 10^{4} \mathrm{~V} \mathrm{~m}^{-1}$. Calculate the separation of the plates.
A potential difference of $2.4 \mathrm{kV}$ is applied across a pair of parallel plates. The electric field strength between the plates is $3.0 \times 10^{4} \mathrm{~V} \mathrm{~m}^{-1}$.
The plates are now moved so that they are $2.0 \mathrm{~cm}$ apart. Calculate the electric field strength produced in this new position.
