Mathematics Crash Course JEE Advanced>Chapter 9 - Parabola>Exercise 1>Q 1

HARD

Mathematics

IMPORTANT

Earn 100

A parabola having directrix $x + y + 2 = 0$ touches a line $2 x + y - 5 = 0$ at $(2, 1)$ . Then the semi-latus rectum of the parabola is

50% studentsanswered this correctly

Important Questions on Parabola

HARD

Mathematics

IMPORTANT

Mathematics Crash Course JEE Advanced>Chapter 9 - Parabola>Exercise 1>Q 2

Slope of the chord of parabola

y^{2} = 4 a x

which passes through the point

(- 6 a, 0)

and which subtends an angle of

45 °

at the vertex, is

HARD

Mathematics

IMPORTANT

Mathematics Crash Course JEE Advanced>Chapter 9 - Parabola>Exercise 1>Q 3

The ends of a line segment are

P (1, 3)

and

Q (1, 1)

.

R

is a point on the line segment

P Q

such that

P R : Q R = 1 : λ

. If

R

is an interior point of the parabola

y^{2} = 4 x

, then

HARD

Mathematics

IMPORTANT

Mathematics Crash Course JEE Advanced>Chapter 9 - Parabola>Exercise 1>Q 4

The distance between the focus and directrix of the conic

(\sqrt{3} x - y)^{2} = 48 (x + \sqrt{3} y)

is

HARD

Mathematics

IMPORTANT

Mathematics Crash Course JEE Advanced>Chapter 9 - Parabola>Exercise 1>Q 5

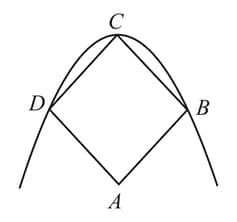
In the adjacent figure, a parabola is drawn to pass through the vertices $B, C$ and $D$ of the square $A B C D$ . If $A (2, 1), C (2, 3)$ , then the focus of this parabola is:

Question Image

HARD

Mathematics

IMPORTANT

Mathematics Crash Course JEE Advanced>Chapter 9 - Parabola>Exercise 1>Q 6

Length of the latus rectum of the parabola

\sqrt{x} + \sqrt{y} = \sqrt{a}

is

HARD

Mathematics

IMPORTANT

Mathematics Crash Course JEE Advanced>Chapter 9 - Parabola>Exercise 1>Q 7

Consider the parabola

x^{2} + 4 y = 0 .

Let

P (a, b)

be any fixed point inside the parabola and let

S

be the focus of the parabola. Then the minimum value of

S Q + P Q

as point

Q

moves on the parabola is

HARD

Mathematics

IMPORTANT

Mathematics Crash Course JEE Advanced>Chapter 9 - Parabola>Exercise 1>Q 8

The line

x - b + λ y = 0

cuts the parabola

y^{2} = 4 a x (a > 0)

at

P (t_{1})

and

Q (t_{2})

. If

b \in [2 a, 4 a]

, then the range of

t_{1} t_{2}

where

λ \in R - {0}

is

HARD

Mathematics

IMPORTANT

Mathematics Crash Course JEE Advanced>Chapter 9 - Parabola>Exercise 1>Q 9

Let a circle touches the directrix of a parabola

y^{2} = 2 a x

has its centre coinciding with the focus of the parabola. Then the point of intersection of the parabola and circle is