A parallel plate capacitor with air as the dielectric has capacitance $C$. A slab of dielectric constant $k$ and having the same thickness as the separation between the plates is introduced to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be



Important Questions on Electrostatics
What will be the capacity of a parallel-plate capacitor when the half-of parallel space between the plates is filled by a material of dielectric constant $\varepsilon_{\mathrm{r}} ?$ Assume that the capacity of the capacitor in air is $C$.
Assertion: A parallel plate capacitor is charged by connecting it across a battery. The battery is then disconnected and separation between the plates is decreased as a result of which the energy stored in the capacitor decreases.
Reason: Energy stored in the capacitor is equal to the work done in charging the capacitor.
If the electric flux leaving and entering an enclosed surface are and , respectively, then the electric charge inside the surface will be
When a charge is enclosed by a closed surface, the flux passing through the surface is . Now another charge is placed inside the closed surface, then the flux passing through the surface is
If there is only one type of charge in the universe, then $(\overrightarrow{\mathrm{E}} \rightarrow$ Electric field, $\overrightarrow{\mathrm{d} s} \rightarrow$ Area of vector $)$
Eight dipoles of charges of magnitude are placed inside a cube. The total electric flux coming out of the cube will be
A positive charge $Q$ is situated at the centre of a cube. The electric flux through any face of the cube is (in SI units)
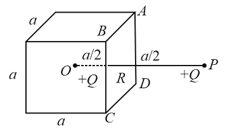
Consider a region in free space bounded by the surfaces of an imaginary cube having sides of length 'a' as shown in the diagram. A charge is placed at the centre of the cube. $P$ is such a point outside the cube that the line perpendicularly intersects the surface $A B C D$ at $R$ and also . A charge is placed at point also. What is the total electric flux through the five faces of the cube other than ?