MEDIUM
Earn 100
A particle enters uniform constant magnetic field region with its initial velocity parallel to the field direction. Which of the following statements about its velocity is correct? (neglect the effects of other fields)
(a)There is change in both magnitude and direction
(b)There is no change
(c)There is change only in magnitude
(d)There is change only in direction
50% studentsanswered this correctly
Important Questions on Magnetic Effect of Current
EASY
EASY
MEDIUM
[Take ]
EASY
EASY
MEDIUM
MEDIUM
Two magnetic dipoles and are placed at a separation , with their axes perpendicular to each other. The dipole moment of is twice that of . A particle of charge is passing through their mid-point , at angle with the horizontal line, as shown in figure. What would be the magnitude of force on the particle at that instant? ( is much larger than the dimension of the dipole)
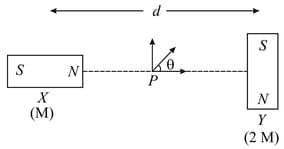
HARD
An electron enters a magnetic field of with a velocity of The acceleration produced is
( of electron )
MEDIUM
MEDIUM
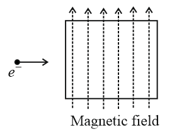
During its motion inside the chamber
MEDIUM
MEDIUM
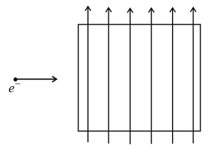
An electric field of appropriate magnitude is also applied so that the electron travels un-deviated without any change in its speed through the chamber. We are ignoring gravity. Then, the direction of the electric field is,
EASY
HARD
EASY
MEDIUM
EASY
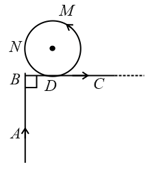
Consider a negatively charged particle moving with a velocity in a magnetic field applied perpendicular to the plane of the paper (into the paper). The particle follows the path or or or (shown in the figure)
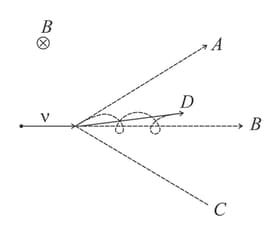
MEDIUM
MEDIUM
HARD

