EASY

JEE Main

IMPORTANT

Earn 100

A particle executes S.H.M., the graph of velocity as a function of displacement is :

66.67% studentsanswered this correctly

Important Questions on Oscillations

EASY

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 11 - Oscillations>JEE Main - 26 Feb 2021 Shift 2>Q 36

A particle executes S.H.M. with amplitude

A

and time period

T

. The displacement of the particle when its speed is half of maximum speed is

\frac{\sqrt{x} A}{2} .

The value of

x

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 11 - Oscillations>JEE Main - 2 September 2020 Shift 2>Q 37

The displacement time graph of a particle executing SHM is given in figure: (sketch is schematic and not to scale)

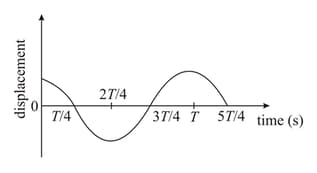
Question Image

Which of the following statements is/are true for this motion?

(A) The force is zero at $t = \frac{3 T}{4}$
(B) The magnitude of acceleration is maximum at $t = T$
(C) The speed is maximum at $t = \frac{T}{4}$
(D) The $P . E .$ is equal to $K . E .$ of the oscillation at $t = \frac{T}{2}$

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 11 - Oscillations>JEE Main - 5 September 2020 Shift 2>Q 38

A ring is hung on a nail. It can oscillate, without slipping or sliding (i) in its plane with a time period

T_{1}

and (ii) back and forth in a direction perpendicular to its plane, with a period

T_{2}

. The ratio

\frac{T_{1}}{T_{2}}

will be :

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 11 - Oscillations>JEE Main - 9th January 2020 Shift 2>Q 39

A spring mass system (mass

m,

spring constant

k

and natural length

l

) rests in equilibrium on a horizontal disc. The free end of the spring is fixed at the centre of the disc. If the disc together with spring mass system rotates about it's axis with an angular velocity

ω, (k > > m ω^{2})

the relative change in the length of the spring is best given by the option:

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 11 - Oscillations>JEE Main - 9th April 2019 Shift 1>Q 40

A simple pendulum oscillating in air has period

T

. The bob of the pendulum is completely immersed in a non-viscous liquid. The density of the liquid is

\frac{1}{16} t h

of the material of the bob. If the bob is inside liquid all the time, its period of oscillation in this liquid is:

HARD

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 11 - Oscillations>JEE Main - 9th January 2019 Shift 1>Q 41

Two masses

m

and

\frac{m}{2}

are connected at the two ends of a massless rigid rod of length

l .

The rod is suspended by a thin wire of torsional constant

k

at the centre of mass of the rod-mass system (see figure). Because of torsional constant

k,

the restoring torque is

τ = k θ

for angular displacement

θ .

If the rod is rotated by

θ_{0}

and released, the tension in it when it passes through its mean position will be:
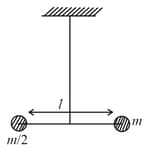
Question Image

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 11 - Oscillations>JEE Main - 9th January 2019 Shift 2>Q 42

A particle is executing simple harmonic motion

(S H M)

of amplitude

A,

along the

x

-axis, about

x = 0 .

When its potential Energy

(P E)

equals kinetic energy

(K E),

the position of the particle will be:

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 11 - Oscillations>JEE Main - 9th January 2019 Shift 2>Q 43

The position co-ordinates of a particle moving in a $3 D$ coordinate system is given by

$x = a \cos ω t$

$y = a \sin ω t$

and $z = a ω t$

The speed of the particle is:

A particle executes S.H.M., the graph of velocity as a function of displacement is :

Important Questions on Oscillations

Learn and Prepare for any exam you want !