Alpha Question Bank for Medical: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-1>Q 98

MEDIUM

NEET

IMPORTANT

Earn 100

A particle is executing simple harmonic motion with angular frequency $ω$ , then the angular frequency of its kinetic energy will be

50% studentsanswered this correctly

Important Questions on Simple Harmonic Motion

EASY

NEET

IMPORTANT

Alpha Question Bank for Medical: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-1>Q 99

In a simple harmonic oscillator, at the mean position

MEDIUM

NEET

IMPORTANT

Alpha Question Bank for Medical: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-1>Q 100

A body executes simple harmonic motion. The potential energy (PE), kinetic energy (KE) and total energy (TE) are measured as a function of displacement ( $x$ ). Which of the following statements is true?

EASY

NEET

IMPORTANT

Alpha Question Bank for Medical: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-1>Q 101

The particle executing simple harmonic motion has a kinetic energy

K_{0} \cos^{2} ω t

. The maximum values of the potential energy and the total energy are respectively (Assuming potential energy to be zero at the mean position)

EASY

NEET

IMPORTANT

Alpha Question Bank for Medical: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-1>Q 102

The total energy of a particle, executing simple harmonic motion is

(Where

x

is the displacement from the mean position.)

HARD

NEET

IMPORTANT

Alpha Question Bank for Medical: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-1>Q 103

A particle of mass $m$ executes simple harmonic motion with amplitude $a$ and frequency $v$ . The average kinetic energy during its motion from the position of equilibrium to the end is

EASY

NEET

IMPORTANT

Alpha Question Bank for Medical: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-1>Q 104

A particle of mass

m

is executing oscillations about the origin on the x-axis. Its potential energy is

U (x) = k {[x]}^{3}

, where

k

is a positive constant. If the amplitude of oscillation is

a

, then its time period

T

is

EASY

NEET

IMPORTANT

Alpha Question Bank for Medical: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-1>Q 105

Two bodies

M

and

N

of equal masses are suspended from two separate massless springs of spring constants

k_{1}

and

k_{2}

, respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of

M

to that on

N

is

EASY

NEET

IMPORTANT

Alpha Question Bank for Medical: Physics>Chapter 19 - Simple Harmonic Motion>Exercise-1>Q 106

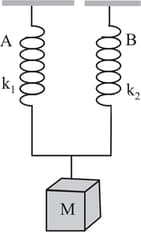
A mass $m$ is suspended by means of two coiled springs which have the same length in unstretched condition as in figure. Their force constants are $k_{1}$ and $k_{2}$ , respectively. When set into vertical vibrations, the period will be,

Question Image