A particle moves in a circle of radius $2.0 \mathrm{cm}$ at a speed given by, $v=4t$, where $v$ is in $\mathrm{cm} {\mathrm{s}}^{-1}$ and $t$ is in seconds.
(a) Find the tangential acceleration at $t=1 \mathrm{s}$.
(b) Find total acceleration at $t=1 \mathrm{s}$.

A particle $P$ moves with a constant speed $v$ in a curve as shown in the figure. Discuss the variation of magnitude of normal acceleration with time and distance.

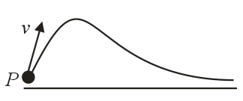
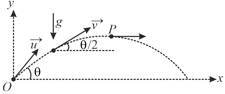
A particle is projected with velocity $u$ at an angle $\theta$ with the horizontal.
(i) Find the tangential and normal acceleration of the particle at $t=0$ and at highest point of its trajectory.
(ii) Find the radius of curvature.
(a) at $O$
(b) at highest position $P.$

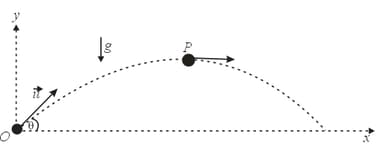
A particle is projected with velocity $u$ at an angle $\theta$ with the horizontal. Find the radius of curvature where its line of motion makes an angle $\frac{\theta }{2}$ with horizontal.

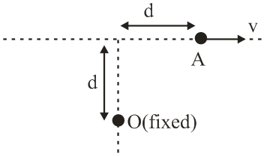
A particle is moving with constant speed in a circle as shown in figure. Find the angular velocity of the particle $A$ with respect to fixed points $B$ and $C$ if angular velocity with respect to $O$ is $\omega$

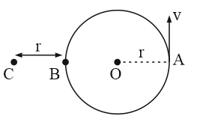
Particles $A$ and $B$ move with constant and equal speeds in a circle as shown in figure. Find the angular velocity of the particle $A$ with respect to $B$, if the angular velocity of particle $A$ with respect to $O$ is $\omega$

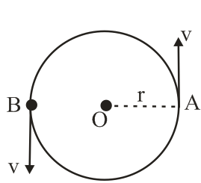
Find the angular velocity of $A$ with respect to $O$ at the instant shown in figure.