For a body projected at an angle with the horizontal from the ground, choose the correct statement

Gravitational potential energy is maximum at the highest point.

The horizontal component of velocity is zero at highest point.

The vertical component of momentum is maximum at the highest point.

The kinetic energy (K.E.) is zero at the highest point of projectile motion.

An object moves with speed v 1 , v 2 and v 3 along a line segment A B , B C and C D respectively as shown in figure. Where A B = B C and A D = 3 A B , then average speed of the object will be :

3 v 1 v 2 v 3 v 1 v 2 + v 2 v 3 + v 3 v 1

v 1 v 2 v 3 3 v 1 v 2 + v 2 v 3 + v 3 v 1

HARD

JEE Main

IMPORTANT

Earn 100

A particle moves such that its position vector $\vec{r} (t) = \cos ω t \hat{i} + \sin ω t \hat{j}$ , where $ω$ is a constant and $t$ is time. Then which of the following statements is true for the velocity $\vec{v} (t)$ and acceleration $\vec{a} (t)$ of the particle:

16% studentsanswered this correctly

Important Questions on Kinematics

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 2 - Kinematics>JEE Main - 8th January 2020 Shift 2>Q 65

A ball is dropped from the top of a

100 m

high tower on a planet. In the last

\frac{1}{2} s

before hitting the ground, it covers a distance of

19 m .

Acceleration due to gravity (in

m s^{- 2}

) near the surface on that planet is______

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 2 - Kinematics>JEE Main - 9th January 2020 Shift 1>Q 66

The distance

x

covered by a particle in one dimensional motion varies with time

t

x^{2} = a t^{2} + 2 b t + c

. If the acceleration of the particle depends on

x

x^{- n}

, where

n

is an integer, the value of

n

is _________

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 2 - Kinematics>JEE Main - 9th January 2020 Shift 1>Q 67

One end of a straight uniform

1 m

long bar is pivoted on horizontal table. It is released from rest when it makes an angle

30^{o}

from the horizontal (see figure). Its angular speed when it hits the table is given as

\sqrt{n} rad s^{- 1}

, where

n

is an integer. The value of

n

is ____________
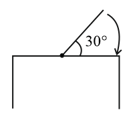
Question Image

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 2 - Kinematics>JEE Main - 9th January 2020 Shift 2>Q 68

A particle starts from the origin at

t = 0

with an initial velocity of

(3.0 \hat{i}) m s^{- 1}

and moves in the

x - y

plane with a constant acceleration

(6.0 \hat{i} + 4.0 \hat{j}) m s^{- 2}

. The

x -

coordinate of the particle at the instant when its

y -

coordinate is

32 m

D

meters. The value of

D

is:

EASY

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 2 - Kinematics>JEE Main - 9th April 2019 Shift 1>Q 69

The stream of a river is flowing with a speed of

2 k m h^{- 1}

. A swimmer can swim at a speed of

4 km h^{- 1}

. The direction of the swimmer with respect to the flow of the river, to cross the river straight, is

HARD

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 2 - Kinematics>JEE Main - 9th April 2019 Shift 2>Q 70

The position of a particle as a function of time

t,

is given by

x (t) = a t + b t^{2} - c t^{3}

where

a, b

and

c

are constants. When the particle has zero acceleration, then its velocity will be:

EASY

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 2 - Kinematics>JEE Main - 9th April 2019 Shift 2>Q 71

The position vector of a particle changes with time according to the relation

\vec{r} (t) = 15 t^{2} \hat{i} + (4 - 20 t^{2}) \hat{j} .

What is the magnitude of the acceleration at

t = 1 ?

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS>Chapter 2 - Kinematics>JEE Main - 9th January 2019 Shift 1>Q 72

A particle is moving with a velocity

\vec{v} = K (y \hat{i} + x \hat{j}),

where

K

is a constant.

The general equation for its path is:

A particle moves such that its position vector r→t=cosωt i^+sinωt j^, where ω is a constant and t is time. Then which of the following statements is true for the velocity v→t and acceleration a→t of the particle:

Important Questions on Kinematics

Learn and Prepare for any exam you want !

A particle moves such that its position vector $\vec{r} (t) = \cos ω t \hat{i} + \sin ω t \hat{j}$ , where $ω$ is a constant and $t$ is time. Then which of the following statements is true for the velocity $\vec{v} (t)$ and acceleration $\vec{a} (t)$ of the particle: