A particle of constant mass moves in straight line under a time varying force. The change in momentum of the particle in a time interval to can be given as
.
The force acting on the particle as a function of time is shown in the graph. If velocity of the particle is zero at , then
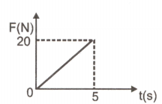
.
The force acting on the particle as a function of time is shown in the graph. If velocity of the particle is zero at , then


Important Questions on Center of Mass
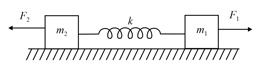
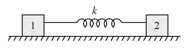
Two blocks initially at rest having masses and are connected by spring of spring constant (as shown in the figure). The block of mass is pulled by a constant force and the other block is pulled by a constant force Find the maximum elongation of the spring.
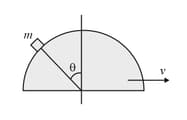
A hemisphere of mass and radius is free to slide with its base on a smooth horizontal table. A particle of mass is placed on the top of the hemisphere. If the particle is displaced with a negligible velocity, then find the angular velocity of the particle relative to the centre of the hemisphere at an angular displacement when the velocity of the hemisphere is .
Two blocks of masses and are connected by spring of constant The spring is initially compressed and the system is released from rest at . The work done by spring on the blocks and be and respectively by time The speeds of both the blocks at time are non-zero.
Then the value of equals to
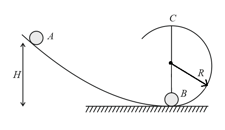
Ball of mass after sliding from an inclined plane strikes elastically to another ball of same mass at rest. Find the minimum height so that ball just completes the circular motion.
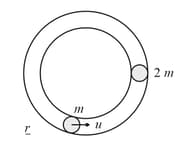
Two masses and are placed in fixed horizontal circular smooth hollow tube as shown. The mass is moving with speed and the mass is stationary. After their first collision, the time elapsed for the next collision. (coefficient of restitution, )