A particle of mass 5 x 10-5 kg is placed at the lowest point of a smooth parabola having the equation x2 = 40y (x, y in cm). If it is displaced slightly and it moves such that it is constrained to move along the parabola, the angular frequency of oscillation will be, approximately
Important Questions on Simple Harmonic Motion
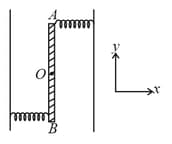
The point moves with a uniform speed along the circumference of a circle of radius and covers in . The perpendicular projection from on the diameter represents the simple harmonic motion of . The restoration force per unit mass when touches will be :
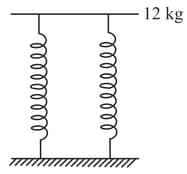
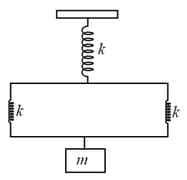
A tray of mass is supported by two identical springs as shown in figure. When the tray is pressed down slightly and then released, it executes SHM with a time period of . The spring constant of each spring is
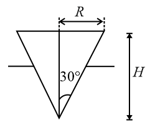
A cone with half the density of water is floating in water as shown in figure. It is depressed down by a small distance and released. The frequency of simple harmonic oscillations of the cone is
A particle of mass and charge is lying at the mid-point of two stationary particles kept at a distance when each is carrying same charge . If the free charged particle is displaced from its equilibrium position through distance . The particle executes SHM. Its angular frequency of oscillation will be _______ (if )
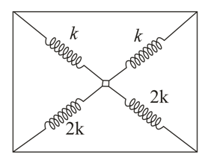
A particle of mass is attached to four springs with spring constant and as shown in the figure. Four springs are attached to the four corners of a square and a particle is placed at the center. If the particle is pushed slightly towards any side of the square and released, the period of oscillation will be
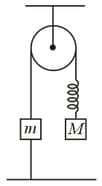
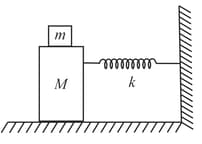
The pulley and the strings are massless and . The spring is light with spring constant . If the string connecting to the ground is detached, then immediately after detachment
In the given figure, a mass is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is The mass oscillates on a frictionless surface with time period and amplitude When the mass is in equilibrium position, as shown in the figure, another mass is gently fixed upon it. The new amplitude of oscillation will be: