A particle rests in equilibrium under two forces of repulsion whose centres are at a distance of $a$ and $b$ from the particle. The forces vary as the cube of the distance. The forces per unit mass are $k$ and $k\text{'}$, respectively. If the particle is slightly displaced towards one of them, the motion is simple harmonic with the time period equal to,

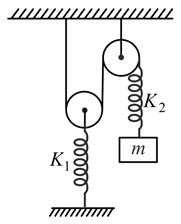
For given spring-mass system, If the time period of small oscillations of block about its mean position is $\pi \sqrt{\frac{nm}{k}}$, then find $n$. Assume ideal conditions. The system is in a vertical plane and take $k_1=2k, k_2=k.$

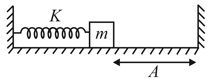
In the figure shown the spring is relaxed and mass m is attached to the spring. The spring is compressed by $2A$ and released at $t= 0$. Mass $m$ collides with the wall and loses two-third of its kinetic energy and returns. Starting from $t= 0$, find the time taken by it to come back to rest again (instant at which spring is again under maximum compression). Take $\sqrt{\frac{m}{K}}=\frac{12}{\pi }$

A block of mass $4 \mathrm{kg}$ attached with spring of spring constant $100 \mathrm{N} {\mathrm{m}}^{-1}$ is executing SHM of amplitude $0.1 \mathrm{m}$ on a smooth horizontal surface as shown in the figure. If another block of mass $5 \mathrm{kg}$ is gently placed on it, at the instant it passes through the mean position and new amplitude of motion is $n^{–1}$ meter then find $n$. Assuming that two blocks always move together. 

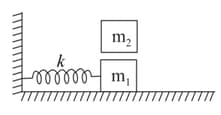
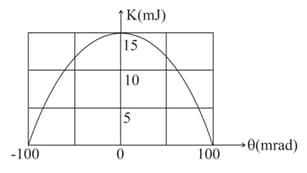
Figure shows the kinetic energy $K$ of a simple pendulum versus its angle $\mathrm{\theta }$ from the vertical. The pendulum bob has mass $0.2 \mathrm{kg}$. If the length of the pendulum is equal to $\frac{\mathit{n}}{\mathit{g}}$ meter, then find $n (g = 10 \mathrm{m} {\mathrm{s}}^{-2}).$

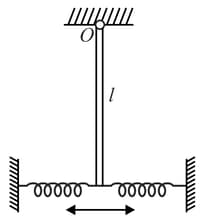
If the angular frequency of small oscillations of a thin uniform vertical rod of mass $m$ and length $l$ hinged at the point $\mathrm{O}$ (Fig.) is $\sqrt{\frac{n}{l}}$, then find $\mathrm{n}$. The force constant for each spring is $K/2$ and take $K=\frac{2mg}{l}.$ The springs are of negligible mass. $(g= 10 \mathrm{m} {\mathrm{s}}^{-2})$