A pendulum is executing simple harmonic motion and its maximum kinetic energy is $K_1.$ If the length of the pendulum is doubled and it performs simple harmonic motion with the same amplitude as in the first case, its maximum kinetic energy is $K_2.$ Then:

A wooden cube (density of wood $d$) of side $l$ floats in a liquid of density $\rho$ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs a simple harmonic motion of period $T$. Then, $T$ is equal to: 

A cylindrical plastic bottle of negligible mass is filled with $310 \mathrm{ml}$ of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic motion at angular frequency, $\omega$. If the radius of the bottle is $2.5 \mathrm{cm}$ then $\omega$ is close to (density of water $={10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$)

A highly rigid cubical block $A$ of small mass $M$ and side $L$ is fixed rigidly on to another cubical block $B$ of the same dimensions and of low modulus of rigidity $\eta$ such that the lower face of $A$ completely covers the upper face of $B$. The lower face of $B$ is rigidly held on a horizontal surface. A small force $F$ is applied perpendicular to one of the side faces of $A$. After the force is withdrawn, block $A$ executes small oscillations, the time-period of which is given by

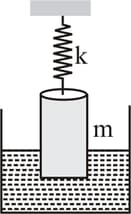
A uniform cylinder of mass $m$ and length $l$ having an area of cross-section $A$ is suspended lengthwise with the help of a massless spring of constant $k$. The cylinder is half-submerged in a liquid of density $\rho$. A small push and release make it vibrate with a small amplitude. The frequency of oscillation is:

A cylindrical piston of mass $M$ slides smoothly inside a long cylinder closed at one end, enclosing a certain mass of a gas. The cylinder is kept with its axis horizontal. If the piston is disturbed from its equilibrium position, it oscillates simple harmonically. The period of oscillation will be (process is isothermal)

A U-tube contains mercury of total length $2l$ as shown and is disturbed so that it oscillates back and forth from arm to arm. If we neglect friction, the period of oscillation is: