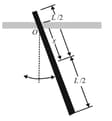
A pendulum is formed by pivoting a long thin rod about a point on the rod. In a series of experiments, the period is measured as a function of the distance between the pivot point and the rod's centre.
(a) If the rod's length is and its mass is , what is the minimum period?
(b) chosen to minimize the period and then is increased, does the period increase, decrease, or remain the same?
(c) If, instead, is increased without increasing, does the period increase, decrease, or remain the same?

Important Questions on Oscillations
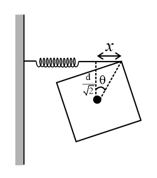
The cube in the figure shown below has edge lengths, and is mounted on an axle through its centre. A spring () connects the cube's upper corner to a rigid wall. Initially the spring is at its rest length. If the cube is rotated and released, what is the period of the resulting ?
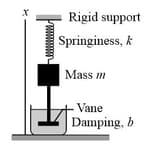
For the damped oscillator system shown in the figure below, the block has a mass of and the spring constant is . The damping force is given by, , where . The block is pulled down and released. (a) Calculate the time required for the amplitude of the resulting oscillations to fall to one-third of its initial value. (b) How many oscillations are made by the block in this time?
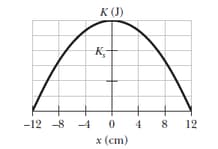
In the figure shown below shows the kinetic energy of a simple harmonic oscillator versus its position . The vertical axis scale is set by . What is the spring constant?