EASY

Earn 100

A person standing on the bank of a river finds that the angle of elevation of the top of a tower on the opposite bank is $45 °$ . Then which of the following statements is correct

50% studentsanswered this correctly

Important Questions on Heights and Distances

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

A B C

is a triangular park with

A B = A C = 100

metres. A vertical tower is situated at the mid-point of

B C

. If the angles of elevation of the top of the tower at,

A

and

B

are

{c o t}^{- 1} (3 \sqrt{2})

and

{c o s e c}^{- 1} (2 \sqrt{2})

respectively, then the height of the tower (in metres) is

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

If the angles of elevation of the top of a tower from three collinear points

A, B

and

C

on a line leading to the foot of the tower are

30 °, 45 °

and

60 °

respectively, then the ratio

A B : B C

, is

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

Two vertical poles of height,

20 m

and

80 m

stand apart on a horizontal plane. The height (in meters) of the point of intersection of the lines joining the top of each pole to the foot of the other, from this horizontal plane is:

EASY

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

Two poles of the height $12 m$ and $17 m$ stand vertically upright on a plain ground. If the distance between their feet is $12 m$ , find the distance between their tops.

HARD

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

A sphere with centre $O$ sits atop a pole as shown in the figure. An observer on the ground is at a distance $50 m$ from the foot of the pole. She notes that the angles of elevation from the observer to points $P$ and $Q$ on the sphere are $30 °$ and $60 °$ , respectively. Then, the radius of the sphere in meters is

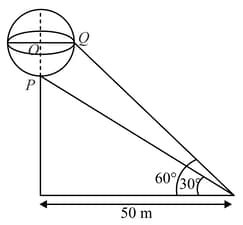
Question Image

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

In triangle

ABC

measure of angle

B

90 °

. If

\sec A = \frac{25}{7}

and

AB = 14 cm

, what is the length (in

cm

) of side

BC

HARD

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

A man is walking towards a vertical pillar in a straight path, at a uniform speed. At a certain point

A

on the path, he observes that the angle of elevation of the top of the pillar is

30^{°}

. After walking for

10

minutes from

A

in the same direction, at a point

B

, he observes that the angle of elevation of the top of the pillar is

60^{°}

. Then the time taken (in minutes) by him, from

B

to reach the pillar, is

HARD

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

A peacock perched on the top of a

12 m

high tree spots a snake moving towards its hole at the base of a tree from a distance equal to thrice the height of the tree. The peacock flies towards the snake in a straight line, and they both move at the same speed. At what distance from the base of the tree will peacock catch the snake?

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

Let a vertical tower

A B

have its end

A

on the level ground. Let

C

be the mid-point of

A B

and

P

be a point on the ground such that

A P = 2 A B

. If

∠ B P C = β

, then

\tan β

is equal to:

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

A man on the top of a vertical tower observes a car moving at a uniform speed towards the tower on a horizontal road. If it takes

18 \min

for the angle of depression of the car to change from

30 °

45 °

, then the time taken (in

\min

) by the car to reach the foot of the tower is

EASY

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

A ladder $10 m$ long is leaning against a vertical wall. It makes an angle of $60 °$ with the ground. How far is the foot of the ladder from the wall?

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

Let

10

vertical poles standing at equal distances on a straight line, subtend the same angle of elevation

α

at a point

O

on this line and all the poles are on the same side of

O

. If the height of the longest pole is

h

and the distance of the foot of the smallest pole from

O

a

; then the distance between two consecutive poles, is

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

X is $5 m$ tall and he notices that he casts a shadow that is $3 m$ long. He then measures that the shadow cast by his school building is $30 m$ long. How tall is the building?

EASY

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

∆ XYZ

, the measure of angle

Y

90 °

. If

\sec X = \frac{17}{8}

, and

XY = 0.8 cm

, what is the length (in

cm

) of side

XZ

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

P and Q are two points on the ground on either side of a pole. The angles of elevation of the top of the pole as observed from P and Q are

60^{o}

and

30^{o}

, respectively and the distance between them is

84 \sqrt{3} m

. What is the height (in

m

) of the pole?

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

A person standing on the top of a building of height

60 \sqrt{3}

feet observed the top of a tower to lie at an elevation of

45 ° .

That person descended to the bottom of the building and found that the top of the same tower is now at an angle of elevation of

60 ° .

The height of the tower (in feet) is

HARD

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

The angle of elevation of a cloud

C

from a point

P, 200 m

above a still lake is

30^{o}

. If the angle of depression of the image of

C

in the lake from the point

P

60^{o}

, then

P C

(in

m

) is equal to

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

P Q R

is a triangular park with

P Q = P R = 200 m

. A T.V. tower stands at the mid-point of

Q R

. If the angles of elevation of the top of the tower at

P, Q

and

R

are respectively,

45 °, 30 °

and

30 °

, then the height of the tower (in

m

) is:

MEDIUM

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

A bird is sitting on the top of a vertical pole

20 m

high and its elevation from a point

O

on the ground is

45 °

. It flies off horizontally straight away from the point

O

. After one second, the elevation of the bird from

O

is reduced to

30 °

. Then the speed (in

m / s

) of the bird is

HARD

Mathematics>Trigonometry>Heights and Distances>Heights and Distances

If the angle of elevation of a cloud from a point

P

which is

25 m

above a lake be

30 °

and the angle of depression of reflection of the could in the lake from

P

60 °

, then the height of the cloud (in meters) from the surface of the lake is :

A person standing on the bank of a river finds that the angle of elevation of the top of a tower on the opposite bank is 45°. Then which of the following statements is correct

Important Questions on Heights and Distances

Learn and Prepare for any exam you want !

A person standing on the bank of a river finds that the angle of elevation of the top of a tower on the opposite bank is $45 °$ . Then which of the following statements is correct