A plano-convex lens of refractive index $n_1$ and focal length $f_1$ is kept in contact with another plano-concave lens of refractive index $n_2$ and focal length $f_2$. If the radius of curvature of their spherical faces is $R$ each and $f_1=2f_2$, then $n_1$ and $n_2$ are related as:

A convex lens is put $10 \mathrm{cm}$ from a light source and it makes a sharp image on a screen, kept $10 \mathrm{cm}$ from the lens. Now a glass block (refractive index $1.5$) of $1.5 \mathrm{cm}$ thickness is placed in contact with the light source. To get the sharp image again, the screen is shifted by a distance $d$. Then $d$ is:

Formation of real image using a biconvex lens is shown below:

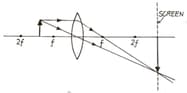
If the whole set-up is immersed in water without disturbing the object and the screen position, what will one observe on the screen?

A plano-convex lens (focal length $f_2$. refractive index $n_2$, radius of curvature $R$) fits exactly into a plano-concave lens (focal length $f_1$’ refractive index $n_1$, radius of curvature $R$). Their plane surfaces are parallel to each other. Then, the focal length of the combination will be:

An object is at a distance of $20 \mathrm{m}$ from a convex lens of focal length $0.3 \mathrm{m}$. The lens forms an image of the object. If the object moves away from the lens at a speed of $5 \raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$s$}\right.$, the speed and direction of the image will be:

Two similar thin equi-convex lenses, of focal length $f$ each, are kept coaxially in contact with each other such that the focal length of the combination is $f_1$. When the space between the two lenses is filled with glycerine (which has the same refractive index ($n=1.5$) as that of glass) then the equivalent focal length is $f_2$. The ratio $f_1:f_2$ will be:

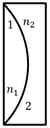
One plano-convex and one plano-concave lens of same radius of curvature ‘$R$’ but of different materials are joined side-by-side as shown in the figure.If the refractive index of the material of $1$ is $n_1$ and that of $2$ is $n_2$, then the focal length of the combination is:

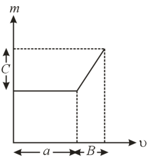
The graph shows how the magnification $m$ produced by a thin lens varies with image distance $u$. What is the focal length of the lens used?